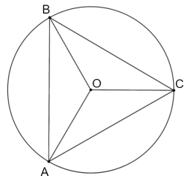
Một phép quay thuận chiều 120° tâm O biến điểm A thành điểm B, biến điểm B thành điểm C
Một phép quay thuận chiều 120° tâm O biến điểm A thành điểm B, biến điểm B thành điểm C. Chứng tỏ rằng ABC là tam giác đều nội tiếp một đường tròn tâm O.
Giải sách bài tập Toán 9 Bài 30: Đa giác đều - Kết nối tri thức
Bài 9.42 trang 60 sách bài tập Toán 9 Tập 2: Một phép quay thuận chiều 120° tâm O biến điểm A thành điểm B, biến điểm B thành điểm C. Chứng tỏ rằng ABC là tam giác đều nội tiếp một đường tròn tâm O.
Lời giải:
Phép quay thuận chiều 120° tâm O biến điểm A thành điểm B nên OA = OB, biến điểm B thành điểm C nên OB = OC, suy ra OA = OB = OC.
Phép quay thuận chiều 120° tâm O biến điểm A thành điểm B, biến điểm B thành điểm C nên các cung có số đo bằng 120°.
Các góc ACB và BAC là các góc nội tiếp của (O) chắn các cung nên
Suy ra
Vậy tam giác ABC là tam giác đều (đpcm).
Lời giải SBT Toán 9 Bài 30: Đa giác đều hay khác:
Bài 9.33 trang 59 sách bài tập Toán 9 Tập 2: Những hình nào dưới đây là đa giác đều? ...
Bài 9.34 trang 59 sách bài tập Toán 9 Tập 2: Hình phẳng nào dưới đây có dạng đa giác đều? ...