Cho O là trung điểm của đoạn thẳng AB. Tìm một phép quay biến điểm A thành điểm B và biến điểm B thành điểm A

Cho O là trung điểm của đoạn thẳng AB.

Giải sách bài tập Toán 9 Bài 30: Đa giác đều - Kết nối tri thức

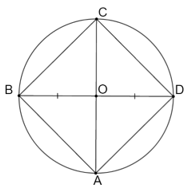
Bài 9.43 trang 60 sách bài tập Toán 9 Tập 2: Cho O là trung điểm của đoạn thẳng AB.

a) Tìm một phép quay biến điểm A thành điểm B và biến điểm B thành điểm A.

b) Phép quay thuận chiều 90° tâm O biến A thành C và biến B thành D. Chứng tỏ rằng ACBD là một hình vuông.

Lời giải:

Cho O là trung điểm của đoạn thẳng AB. Tìm một phép quay biến điểm A thành điểm B và biến điểm B thành điểm A

a) Phép quay thuận chiều 180° tâm O biến điểm A thành điểm B và biến điểm B thành điểm A.

b) O là trung điểm AB nên OA = OB.

Phép quay thuận chiều 90° tâm O biến A thành C và biến B thành D nên OA = OC và OB = OD.

Do đó OA = OB = OC = OD, suy ra tứ giác ABCD nội tiếp đường tròn (O) đường kính AB.

Do $\hat{A O C} = \hat{B O D} = 90 °$ nên OC và OD cùng vuông góc với AB hay C, O, D thẳng hàng.

Suy ra CD là đường kính của (O).

Các góc ACB, CBD, BDA, DAC là các góc nội tiếp chắn nửa đường tròn (O) nên $\hat{A C B} = \hat{C D B} = \hat{B D A} = \hat{D A C} = 90 °$

Do đó ABCD là hình chữ nhật.

Xét tam giác AOC và COB có:

$\hat{A O C} = \hat{C O B} = 90 °$

OA = OC (vì đều bằng bán kính đường tròn);

OC = OB (vì đều bằng bán kính đường tròn).

Suy ra ∆AOC = ∆COB (c.g.c).

Tương tự, ta suy ra ∆AOC = ∆COB = ∆BOD = ∆DOA.

Do đó AC = CB = BD = DA.

Vậy ABCD là hình vuông (đpcm).

Lời giải SBT Toán 9 Bài 30: Đa giác đều hay khác: