Cho tam giác ABC nội tiếp đường tròn (O). Tính số đo của các góc BOC, COA, AOB

Cho tam giác ABC nội tiếp đường tròn (O). Tính số đo của các góc , biết rằng

Giải sách bài tập Toán 9 Bài tập cuối chương 9 - Kết nối tri thức

Bài 9.45 trang 61 sách bài tập Toán 9 Tập 2: Cho tam giác ABC nội tiếp đường tròn (O). Tính số đo của các góc $\widehat{BOC}, \widehat{COA}, \widehat{AOB}$, biết rằng $\widehat{A}=60°, \widehat{B}=70°$

Lời giải:

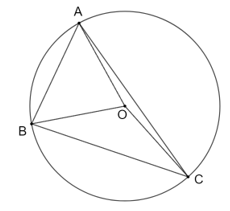
Xét tam giác ABC có $\widehat{BAC}+\widehat{CBA}+\widehat{BCA}=180°$ (định lý tổng ba góc trong một tam giác)

Suy ra $\widehat{ACB}=180°-\widehat{BAC}-\widehat{CBA}=180°-60°-70°=50°$

Xét đường tròn (O) có:

Góc nội tiếp BAC và góc ở tâm BOC cùng chắn cung nhỏ $\stackrel{⏜}{BC}$ nên $\widehat{BOC}=2\widehat{BAC}=2.60°=120°$

Góc nội tiếp CBA và góc ở tâm COA cùng chắn cung nhỏ $\stackrel{⏜}{AC}$ nên $\widehat{COA}=2\widehat{CBA}=2.70°=140°$

Góc nội tiếp ACB và góc ở tâm AOB cùng chắn cung nhỏ $\stackrel{⏜}{AB}$ nên $\widehat{AOB}=2\widehat{ACB}=2.50°=100°$

Vậy $\widehat{BOC}=120°, \widehat{COA}=140°, \widehat{AOB}=100°$

Lời giải SBT Toán 9 Bài tập cuối chương 9 hay khác:

• Bài 1 trang 61 sách bài tập Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp một đường tròn với $\widehat{A}= 70°, \widehat{B}= 100°$. Khẳng định nào dưới đây là đúng? ...

• Bài 2 trang 61 sách bài tập Toán 9 Tập 2: Xét trong một đường tròn, khẳng định nào dưới đây là không đúng? ...

• Bài 3 trang 61 sách bài tập Toán 9 Tập 2: Cho hình chữ nhật ABCD nội tiếp (O) với AB = 4 cm, BC = 3 cm. Đường tròn (O) có bán kính là ...

• Bài 9.44 trang 61 sách bài tập Toán 9 Tập 2: Xét trong một đường tròn, những câu nào dưới đây là đúng? ...

• Bài 9.46 trang 61 sách bài tập Toán 9 Tập 2: Cho tam giác ABC ngoại tiếp đường tròn (I). Đường tròn (I) tiếp xúc các cạnh BC, CA, AB tại D, E, F. Chứng tỏ rằng IEAF, IFBD, IDCE là các tứ giác nội tiếp. ...

• Bài 9.47 trang 61 sách bài tập Toán 9 Tập 2: Cho tam giác đều ABC nội tiếp một đường tròn bán kính 4 cm. Hãy tính độ dài mỗi cạnh và bán kính đường tròn nội tiếp của tam giác ABC. ...

• Bài 9.48 trang 62 sách bài tập Toán 9 Tập 2: Tính diện tích tam giác vuông cân, nội tiếp đường tròn bán kính 4 cm. ...

• Bài 9.49 trang 62 sách bài tập Toán 9 Tập 2: Cho tam giác ABC vuông tại A có diện tích là 24 cm và nội tiếp đường tròn có bán kính 5 cm. Tính bán kính đường tròn nội tiếp tam giác ABC. ...

• Bài 9.50 trang 62 sách bài tập Toán 9 Tập 2: Hãy cho biết số đo các góc còn lại của tứ giác nội tiếp ABCD trong mỗi trường hợp sau: ...

• Bài 9.51 trang 62 sách bài tập Toán 9 Tập 2: Cho tam giác nhọn ABC có đường cao AH. Các điểm M và N lần lượt là hình chiếu vuông góc của H trên AB, AC. Chứng minh rằng AM . AB = AN . AC. ...

• Bài 9.52 trang 62 sách bài tập Toán 9 Tập 2: Cho tam giác nhọn ABC (AB < AC) có các đường cao AD, BE, CF. Cho EF cắt BC tại K. Chứng minh rằng: ...

• Bài 9.53 trang 62 sách bài tập Toán 9 Tập 2: Cho một lục giác đều và một tam giác đều cùng nội tiếp một đường tròn. Biết rằng tam giác đều có cạnh bằng 3 cm ...

• Bài 9.54 trang 62 sách bài tập Toán 9 Tập 2: Cho đa giác đều ϰ có 12 cạnh, nội tiếp một đường tròn (O). Kẻ các đoạn thẳng nối O với các đỉnh của ϰ và thu được 12 góc nhọn tại đỉnh O ...