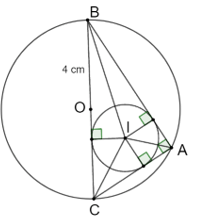
Cho tam giác ABC vuông tại A có diện tích là 24 cm và nội tiếp đường tròn có bán kính 5 cm
Cho tam giác ABC vuông tại A có diện tích là 24 cm và nội tiếp đường tròn có bán kính 5 cm. Tính bán kính đường tròn nội tiếp tam giác ABC.
Giải sách bài tập Toán 9 Bài tập cuối chương 9 - Kết nối tri thức
Bài 9.49 trang 62 sách bài tập Toán 9 Tập 2: Cho tam giác ABC vuông tại A có diện tích là 24 cm và nội tiếp đường tròn có bán kính 5 cm. Tính bán kính đường tròn nội tiếp tam giác ABC.
Lời giải:
Tam giác ABC nội tiếp đường tròn có bán kính 5 cm nên BC là đường kính của đường tròn đó, suy ra BC = 2 . 5 = 10 (cm).
Áp dụng định lý Pythagore vào tam giác vuông ABC ta có:
AB2 + AC2 = BC2 hay AB2 + AC2 = 102 = 100 (cm2)
Diện tích tam giác ABC bằng 24 cm2 nên
(cm2) hay AB . AC = 48 (cm2)
Suy ra (AB + AC)2 = AB2 + AC2 + 2AB . AC = 100 + 2 . 48 = 196.
Do đó AB + AC = 14 (cm).
Gọi I là tâm đường tròn nội tiếp tam giác ABC và r là bán kính của đường tròn đó.
Khi đó r cũng đồng thời là chiều cao hạ từ I xuống các cạnh BC, CA, AB của các tam giác BIC, CIA, AIB.
Ta có:
Do đó 24 = 12r hay r = 2 (cm).
Vậy bán kính đường tròn nội tiếp tam giác ABC là 2 cm.
Lời giải SBT Toán 9 Bài tập cuối chương 9 hay khác: