Bài 1 trang 30 Toán 10 Tập 1 Cánh diều
Biểu diễn miền nghiện của bất phương trình:
Giải Toán lớp 10 Bài tập cuối chương 2
Bài 1 trang 30 Toán lớp 10 Tập 1: Biểu diễn miền nghiện của bất phương trình:
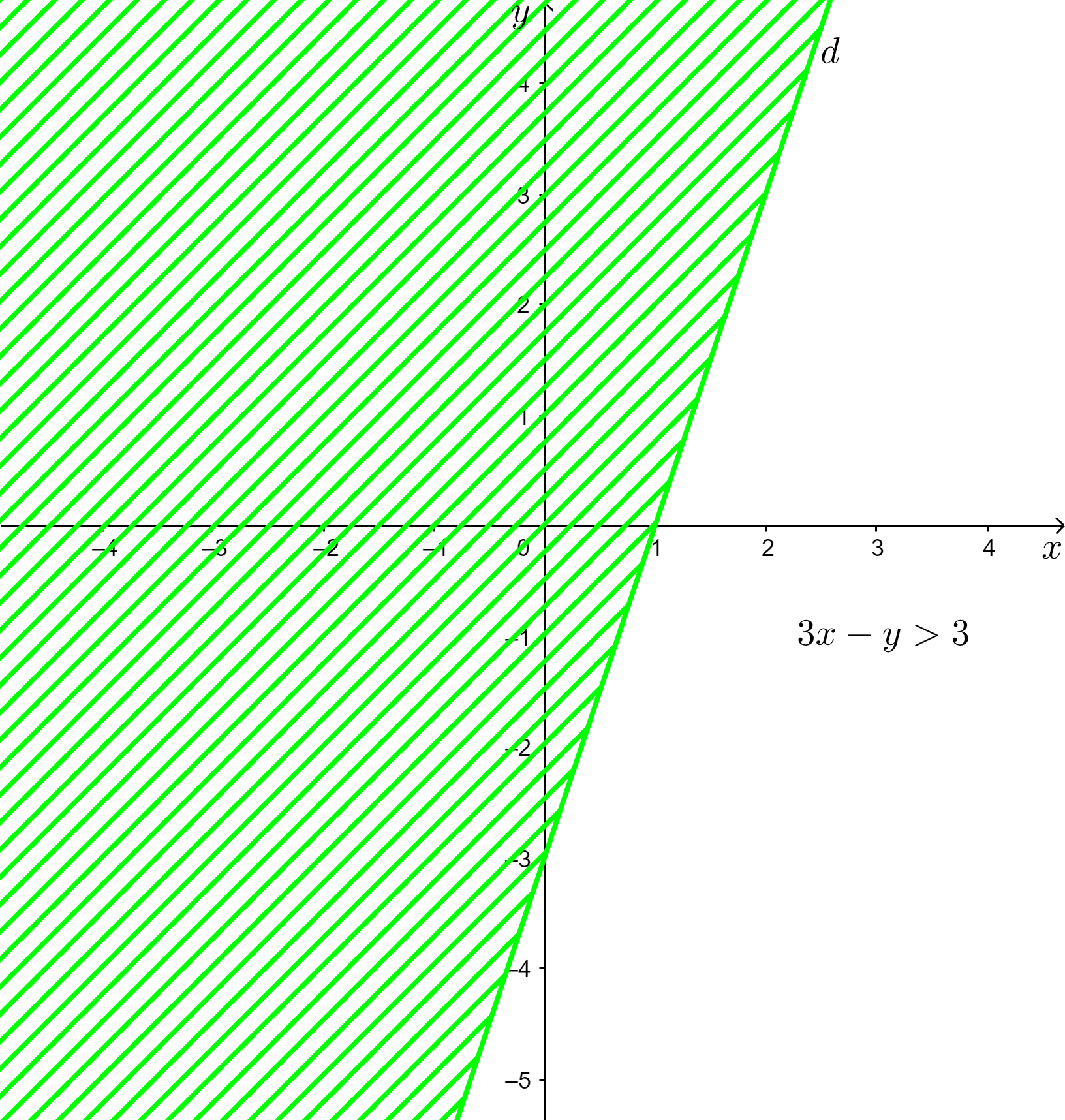
a) 3x – y > 3;
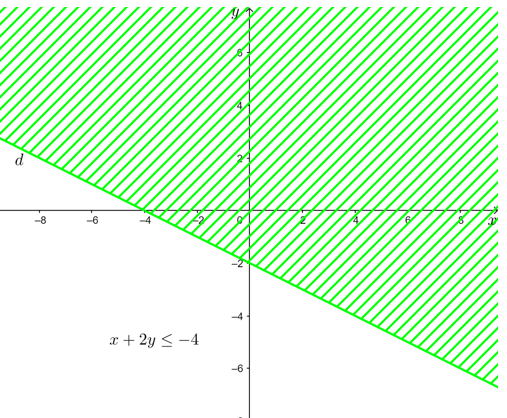
b) x + 2y ≤ – 4;
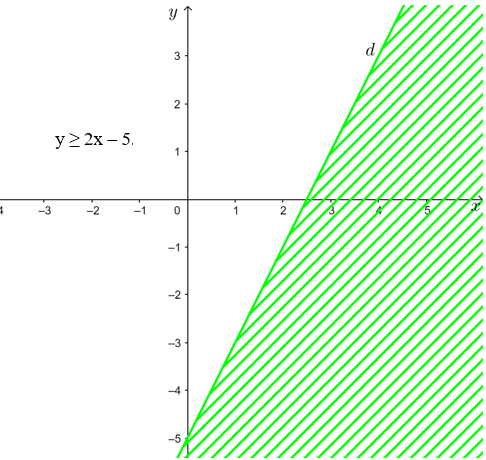
c) y ≥ 2x – 5.
Lời giải:
a) 3x – y > 3
+ Vẽ đường thẳng d: 3x – y = 3.
Đường thẳng d đi qua hai điểm (0; – 3) và (1; 0).
+ Lấy điểm O(0; 0). Ta có: 3 . 0 – 0 = 0 < 3.
Vậy miền nghiệm của bất phương trình 3x – y > 3 là nửa mặt phẳng không bị gạch ở hình trên không chứa điểm O(0; 0) không kể đường thẳng d.
b) x + 2y ≤ – 4
+ Vẽ đường thẳng d: x + 2y = – 4.
Đường thẳng d đi qua 2 điểm (0; – 2) và (– 4; 0).
+ Lấy điểm O(0; 0). Ta có: 0 + 2. 0 = 0 > – 4.
Vậy miền nghiệm của bất phương trình x + 2y ≤ – 4 là nửa mặt phẳng không bị gạch ở hình trên không chứa điểm O(0; 0) kể cả đường thẳng d.
c) y ≥ 2x – 5
⇔ 2x – y ≤ 5
+ Vẽ đường thẳng d: 2x – y = 5.
Đường thẳng d đi qua hai điểm (0; – 5) và (2,5; 0).
+ Lấy điểm O(0; 0). Ta có: 2 . 0 – 0 = 0 < 5.
Vậy miền nghiệm của bất phương trình 2x – y ≤ 5 hay y ≥ 2x – 5 là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) kể cả đường thẳng d.
Lời giải bài tập Toán 10 Bài tập cuối chương 2 hay, chi tiết khác: