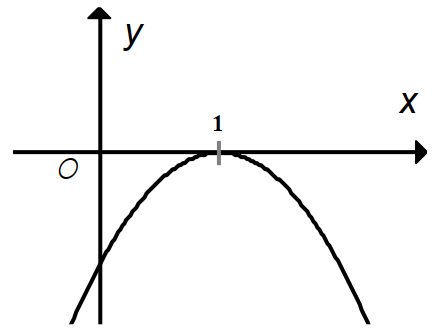
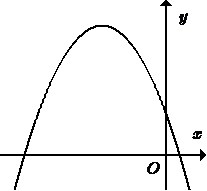Đồ thị sau đây là đồ thị của hàm số nào trong các phương án dưới đây?
Câu hỏi:
Đồ thị sau đây là đồ thị của hàm số nào trong các phương án dưới đây?
A.
B.
C.
D.
Trả lời:
Đáp án đúng là: B
Bề lõm quay xuống nên a < 0 ta loại C, D.
Đồ thị hàm số đi qua điểm , thay x = 1; y = 0 vào các hàm số còn lại ta được:
- Xét hàm số ta có:
0 = + 2.1 = 1 (Vô lý) như vậy điểm (1; 0) không thuộc đồ thị
- Xét hàm số ta có:
0 = + 2.1 - 1 = 0 như vậy điểm (1; 0) thuộc đồ thị hàm số.
Xem thêm bài tập Toán 10 CD có lời giải hay khác:
Câu 1:
Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?
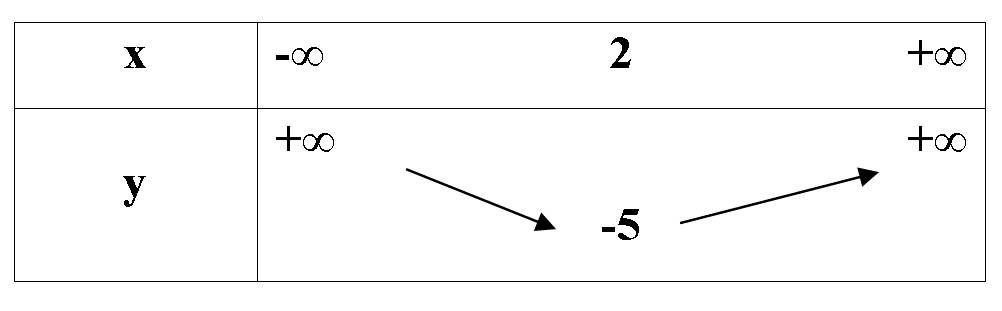
Xem lời giải »
Câu 2:
Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?
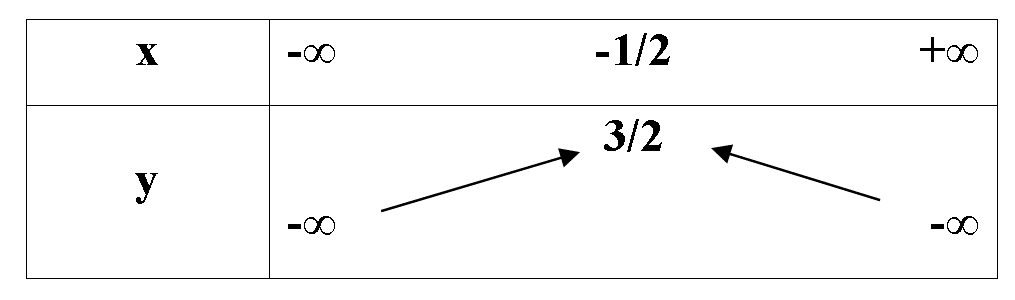
Xem lời giải »
Câu 3:
Bảng biến thiên của hàm số là bảng nào trong các bảng được cho sau đây ?
Xem lời giải »
Câu 4:
Đồ thị sau đây là đồ thị của hàm số nào trong các phương án dưới đây?
Xem lời giải »
Câu 5:
Cho hàm số có đồ thị như hình sau. Khẳng định nào sau đây đúng?
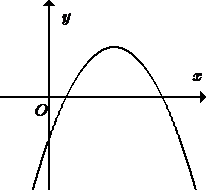
Xem lời giải »
Câu 6:
Cho hàm số có đồ thị như hình sau. Khẳng định nào sau đây đúng?
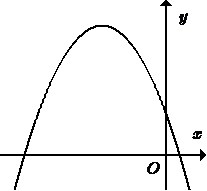
Xem lời giải »
Câu 7:
Cho parabol . Xét dấu hệ số a và biệt thức khi hoàn toàn nằm phía trên trục hoành.
Xem lời giải »
Câu 8:
Cho parabol . Xét dấu hệ số a và biệt thức khi cắt trục hoành tại hai điểm phân biệt và có đỉnh nằm phía trên trục hoành.
Xem lời giải »