Giải Toán 10 trang 54 Tập 1 Cánh diều

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 54 Tập 1 trong Bài 4: Bất phương trình bậc hai một ẩn Toán lớp 10 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 54.

Giải Toán 10 trang 54 Tập 1 Cánh diều

Bài 1 trang 54 Toán lớp 10 Tập 1: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc hai một ẩn? Vì sao?

a) – 2x + 2 < 0; 

b) $\frac{1}{2}{y}^2-\sqrt{2}\left(y+1\right)\le 0$;

c) y² + x² – 2x ≥ 0. 

Lời giải:

a) Bất phương trình – 2x + 2 < 0 không phải là bất phương trình bậc hai một ẩn, đây là bất phương trình bậc nhất một ẩn. 

b) $\frac{1}{2}{y}^2-\sqrt{2}\left(y+1\right)\le 0\iff \frac{1}{2}{y}^2-\sqrt{2}y-\sqrt{2}\le 0$, đây là bất phương trình bậc hai một ẩn với ẩn y. 

c) Bất phương trình y² + x² – 2x ≥ 0 không phải là bất phương trình bậc hai một ẩn, do nó có hai ẩn x và y.

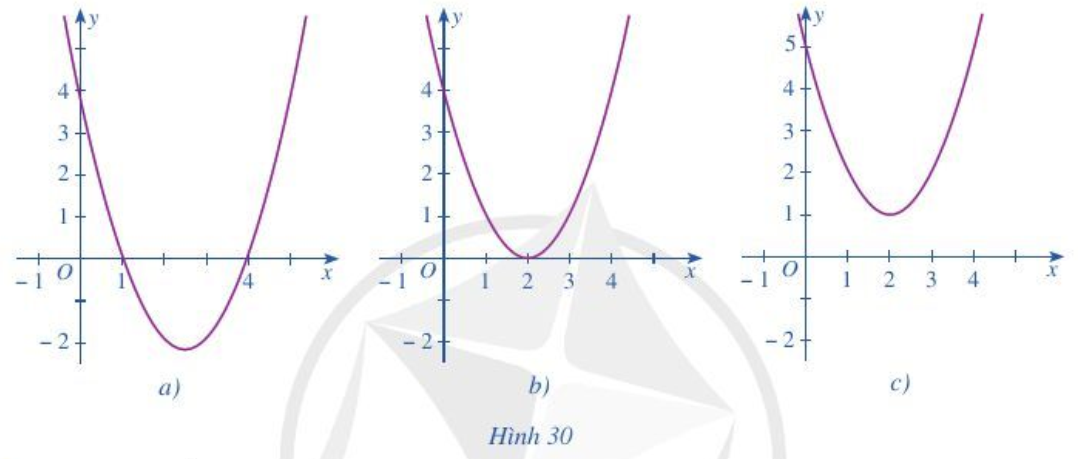
Bài 2 trang 54 Toán lớp 10 Tập 1: Dựa vào đồ thị hàm số bậc hai y = f(x) trong mỗi Hình 30a, 30b, 30c, hãy viết tập nghiệm của mỗi bất phương trình sau: f(x) > 0, f(x) < 0; f(x) ≥ 0; f(x) ≤ 0.

Lời giải:

a) Quan sát đồ thị Hình 30 a, ta thấy: 

+ f(x) > 0 biểu diễn phần parabol y = f(x) nằm phía trên trục hoành, tương ứng với x < 1 hoặc x > 4.

Do đó tập nghiệm của bất phương trình f(x) > 0 là (– ∞; 1) ∪ (4; + ∞). 

Và tập nghiệm của bất phương trình f(x) ≥ 0 là (– ∞; 1] ∪ [4; + ∞). 

+ f(x) < 0 biểu diễn phần parabol y = f(x) nằm phía dưới trục hoành, tương ứng với 1 < x < 4. 

Do đó tập nghiệm của bất phương trình f(x) < 0 là (1; 4). 

Và tập nghiệm của bất phương trình f(x) ≤ 0 là [1; 4]. 

b) Quan sát đồ thị Hình 30 b, ta thấy: 

Tại x = 2 thì f(x) = 0.

+ f(x) > 0 biểu diễn phần parabol y = f(x) nằm phía trên trục hoành, tương ứng với x ≠ 2.

Do đó tập nghiệm của bất phương trình f(x) > 0 là $ℝ\backslash \left\{2\right\}$.

Và tập nghiệm của bất phương trình f(x) ≥ 0 là $\mathrm{ℝ}$.

+ f(x) < 0 biểu diễn phần parabol y = f(x) nằm phía dưới trục hoành, mà phần đồ thị nằm phía trên trục hoành.

Do đó bất phương trình f(x) < 0 vô nghiệm.

Và nghiệm của bất phương trình f(x) ≤ 0 là x = 2. 

c) Quan sát đồ thị Hình 30 c, ta thấy phần parabol nằm hoàn toàn phía trên trục hoành, do đó f(x) > 0 với mọi $x\in ℝ$.

Vậy tập nghiệm của bất phương trình f(x) > 0 là $x\in ℝ$ và các bất phương trình f(x) < 0, f(x) ≥ 0, f(x) ≤ 0 vô nghiệm. 

Bài 3 trang 54 Toán lớp 10 Tập 1: Giải các bất phương trình sau:

a) 2x² – 5x + 3 > 0;

b) – x² – 2x + 8 ≤ 0; 

c) 4x² – 12x + 9 < 0; 

d) – 3x² + 7x – 4 ≥ 0.

Lời giải:

a) 2x² – 5x + 3 > 0

Tam thức bậc hai 2x² – 5x + 3 có hai nghiệm x₁ = 1, x₂ = $\frac{3}{2}$ và có hệ số a = 2 > 0.

Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho tam thức 2x² – 5x + 3 mang dấu “+” là x < 1 hoặc x > $\frac{3}{2}$;.

Vậy tập nghiệm của bất phương trình 2x² – 5x + 3 > 0 là $\left(-\infty ;1\right)\cup \left(\frac{3}{2};+\infty \right).$

b) – x² – 2x + 8 ≤ 0 

Tam thức bậc hai – x² – 2x + 8 có hai nghiệm là x₁ = – 4, x₂ = 2 và hệ số a = – 1 < 0. 

Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho tam thức – x² – 2x + 8 không dương là x ≤ – 4 hoặc x ≥ 2. 

Vậy tập nghiệm của bất phương trình – x² – 2x + 8 là (– ∞; – 4] ∪ [2; + ∞). 

c) 4x² – 12x + 9 < 0 

Tam thức bậc hai 4x² – 12x + 9 có ∆ = (– 12)² – 4 . 4 . 9 = 0. 

Do đó tam thức trên có nghiệm kép là x = $\frac{3}{2}$.

Lại có hệ số a = 4 > 0. 

Sử dụng định lý về dấu của tam thức bậc hai ta có: 4x² – 12x + 9 > 0 với mọi $x\in ℝ\backslash \left\{\frac{3}{2}\right\}$ và 4x² – 12x + 9 = 0 tại x = $\frac{3}{2}$.

Vậy không tồn tại giá trị nào của x để 4x² – 12x + 9 < 0 hay bất phương trình đã cho vô nghiệm.

d) – 3x² + 7x – 4 ≥ 0

Tam thức bậc hai – 3x² + 7x – 4 có hai nghiệm x₁ = 1, x₂ = $\frac{4}{3}$ và hệ số a = – 3 < 0. 

Sử dụng định lý về dấu của tam thức bậc hai, ta thấy – 3x² + 7x – 4 không âm khi $1\le x\le \frac{4}{3}$. 

Vậy tập nghiệm của bất phương trình – 3x² + 7x – 4 ≥ 0 là $\left[1;\frac{4}{3}\right]$.

Bài 4 trang 54 Toán lớp 10 Tập 1: Tìm m để phương trình 2x² + (m + 1)x + m – 8 = 0 có nghiệm.

Lời giải:

Phương trình 2x² + (m + 1)x + m – 8 = 0 (1) là phương trình bậc hai một ẩn với ẩn x và m là tham số.

Ta có: a = 2, b = m + 1, c = m – 8 và 

∆ = (m + 1)² – 4 . 2 . (m – 8) = m² + 2m + 1 – 8m + 64 = m² – 6m + 65.

Phương trình (1) có nghiệm khi và chỉ khi ∆ ≥ 0 

⇔ m² – 6m + 65 ≥ 0, đây là bất phương trình bậc hai một ẩn với ẩn m.

Ta giải bất phương trình trên. 

Tam thức bậc hai m² – 6m + 65 có ∆_m = (– 6)² – 4 . 1 . 65 = – 224 < 0 và hệ số a_m = 1 > 0. 

Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tam thức m² – 6m + 65 mang dấu dương với mọi  . 

Do đó m² – 6m + 65 > 0 với mọi số thực m. 

Vậy phương trình (1) luôn có nghiệm với mọi giá trị thực của m. 

Bài 5 trang 54 Toán lớp 10 Tập 1: Xét hệ tọa độ Oth trên mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây) và trục Oh biểu thị độ cao h (tính bằng mét). Một quả bóng được đá lên từ điểm A(0; 0,2) và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8,5 m sau 1 giây và đạt độ cao 6 m sau 2 giây.

a) Hãy tìm hàm số bậc hai biểu thị quỹ đạo chuyển động của quả bóng. 

b) Trong khoảng thời gian nào thì quả bóng vẫn chưa chạm đất? 

Lời giải:

a) Giả sử hàm số có dạng: h = at² + bt + c, trong đó h là độ cao, t là thời gian, a, b, c là các hằng số cần tìm với a ≠ 0. 

Quỹ đạo của quả bóng là một parabol đi qua điểm A(0; 0,2) nên thay t = 0 và h = 0,2 vào hàm số ta được: c = 0,2. 

Khi đó: h = at² + bt + 0,2

Lại có quả bóng đạt độ cao 8,5 m sau 1 giây và 6 m sau 2 giây, do đó quỹ đạo của bóng là parabol đi qua các điểm có tọa độ (1; 8,5) và (2; 6). 

Ta có hệ: $\left\{\begin{array}{l}a+b+0,2=8,5\\ 2^2.a+b.2+0,2=6\end{array}\right.$

Giải hệ trên ta được: a = – 5,4, b = 13,7 . 

Vậy hàm số bậc hai biểu thị quỹ đạo chuyển động của quả bóng là: h = – 5,4t² + 13,7t + 0,2. 

b) Bóng chạm đất nếu khi độ cao h = 0, vậy bóng chưa chạm đất khi độ cao h > 0. 

Hay – 5,4t² + 13,7t + 0,2 > 0, đây là bất phương trình bậc hai một ẩn với ẩn t. 

Tam thức bậc hai – 5,4t² + 13,7t + 0,2 có hai nghiệm t₁ = $\frac{137}{108}-\frac{\sqrt{19201}}{108}$, $t_2=\frac{137}{108}+\frac{\sqrt{19201}}{108}$.

Sử dụng định lí về dấu của tam thức bậc hai ta có – 5,4t² + 13,7t + 0,2 > 0

$\iff \frac{137}{108}-\frac{\sqrt{19201}}{108}<t<\frac{137}{108}+\frac{\sqrt{19201}}{108}$

Lại có: thời gian t > 0

Do đó: $0<t<\frac{137}{108}+\frac{\sqrt{19201}}{108}$

Mà $\frac{137}{108}+\frac{\sqrt{19201}}{108}\approx 2,55$

Vậy trong khoảng thời gian từ 0 đến 2,55 giây thì bóng vẫn chưa chạm đất. 

Bài 6 trang 54 Toán lớp 10 Tập 1: Công ty An Bình thông báo giá tiền cho chuyến đi tham quan của một nhóm khách du lịch như sau:

10 khách đầu tiên có giá vé là 800 000 đồng/người. Nếu có nhiều hơn 10 người đăng kí thì cứ có thêm 1 người, giá vẽ sẽ giảm 10 000 đồng/người cho toàn bộ hành khách.

a) Gọi x là số lượng khách từ người thứ 11 trở lên của nhóm. Biểu thị doanh thu theo x. 

b) Số người của nhóm khách du lịch nhiều nhất là bao nhiêu thì công ty không bị lỗ? Biết rằng chi phí thực sự cho chuyến đi là 700 000 đồng/người.

Lời giải:

a) x là số lượng khách từ người thứ 11 trở lên của nhóm. (x ∈ ℕ^*)

Tổng số khách là: 10 + x  (người)

Nếu có nhiều hơn 10 người đăng kí thì cứ có thêm 1 người, giá vẽ sẽ giảm 10 000 đồng/người cho toàn bộ hành khách, do đó giá tiền cho chuyến đi của một người khi có 10 + x người tham gia là: 800 000 – 10 000x (đồng).

Khi đó doanh thu của công ty là: y = (800 000 – 10 000x)(10 + x) 

⇔ y = 8 000 000 + 800 000x – 100 000x – 10 000x² 

⇔ y = – 10 000x² + 700 000x + 8 000 000

Vậy doanh thu của công ty theo x là: y = – 10 000x² + 700 000x + 8 000 000. 

b) Chi phí thực sự cho chuyến đi là 700 000 đồng/người nên tổng chi phí cho 10 + x người tham gia là 700 000(10 + x) (đồng).

Để công ty không bị lỗ thì doanh thu phải lớn hơn hoặc bằng tổng chi phí. 

Do đó y ≥ 700 000(10 + x) 

⇔ – 10 000x² + 700 000x + 8 000 000 ≥ 700 000(10 + x) 

⇔ – 10 000x² + 1 000 000 ≥ 0 

⇔ x² – 100 ≤ 0

Áp dụng định lý dấu của tam thức bậc hai, ta giải được bất phương trình trên. 

Ta có: x² – 100 ≤ 0 ⇔ – 10 ≤ x ≤ 10, 

Mà x là số tự nhiên nên 0 ≤ x ≤ 10.

Do đó thêm nhiều nhất là 10 người nữa thì công ty không bị lỗ hay số người của nhóm khách du lịch lúc này là 10 + 10 = 20 người. 

Vậy số người có nhóm du lịch nhiều nhất 20 người thì công ty không bị lỗ. 

Lời giải bài tập Toán lớp 10 Bài 4: Bất phương trình bậc hai một ẩn Cánh diều hay khác:

• Giải Toán 10 trang 49 Tập 1
• Giải Toán 10 trang 50 Tập 1
• Giải Toán 10 trang 51 Tập 1
• Giải Toán 10 trang 53 Tập 1