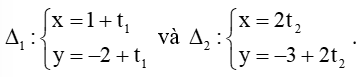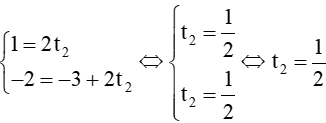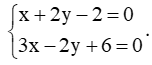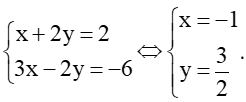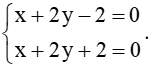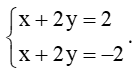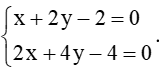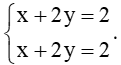Giải Toán 10 trang 82 Tập 2 Cánh diều
Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 82 Tập 2 trong Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng Toán lớp 10 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 82.
Giải Toán 10 trang 82 Tập 2 Cánh diều
Luyện tập 1 trang 82 Toán lớp 10 Tập 2: Xét vị trí tương đối của hai đường thẳng
Lời giải:
Đường thẳng ∆1 có vectơ chỉ phương là .
Đường thẳng ∆2 có vectơ chỉ phương là .
Ta có: , do đó cùng phương.
Chọn t1 = 0, ta có điểm M(1; – 2) thuộc ∆1. Thay tọa độ điểm M vào phương trình ∆2, ta được:
Vậy điểm M cũng thuộc ∆2.
Vậy hai đường thẳng ∆1 và ∆2 trùng nhau.
Luyện tập 2 trang 82 Toán lớp 10 Tập 2: Xét vị trí tương đối của đường thẳng d: x + 2y – 2 = 0 với mỗi đường thẳng sau
Δ1: 3x – 2y + 6 = 0;
Δ2: x + 2y + 2 = 0;
Δ3: 2x + 4y – 4 = 0.
Lời giải:
* Tọa độ giao điểm của đường thẳng d và đường thẳng ∆1 là nghiệm của hệ phương trình:
Phương trình trên tương đương với
Hệ có nghiệm duy nhất là (x; y) = .
Do đó đường thẳng d cắt đường thẳng ∆1 tại điểm có tọa độ .
* Tọa độ giao điểm của đường thẳng d và đường thẳng ∆2 là nghiệm của hệ phương trình:
Phương trình trên tương đương với
Hệ trên vô nghiệm.
Do đó đường thẳng d và đường thẳng ∆2 song song với nhau.
* Tọa độ giao điểm của đường thẳng d và đường thẳng ∆3 là nghiệm của hệ phương trình:
Phương trình trên tương đương với
Hệ trên có vô số nghiệm.
Do đó, hai đường thẳng d và ∆3 có vô số điểm chung nên d trùng với ∆3.
Lời giải bài tập Toán lớp 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng Cánh diều hay khác: