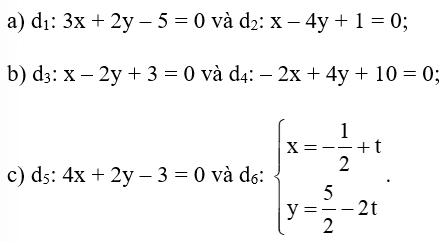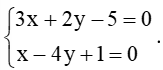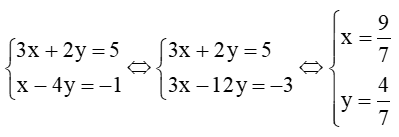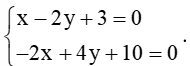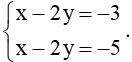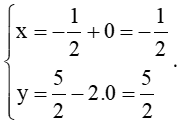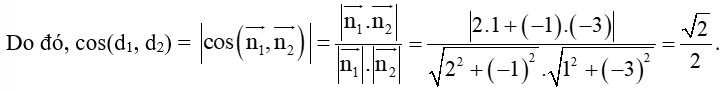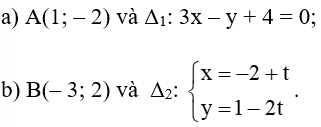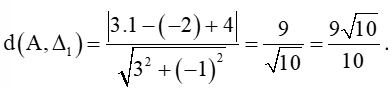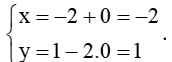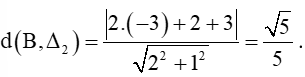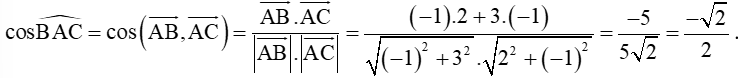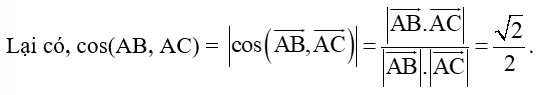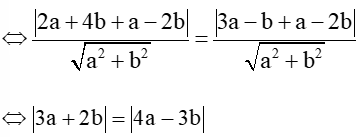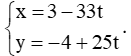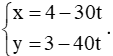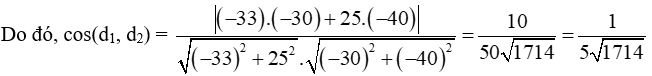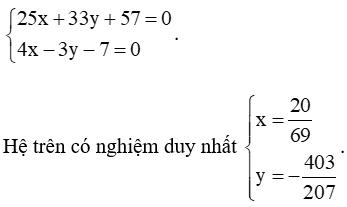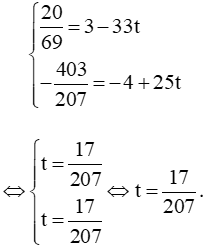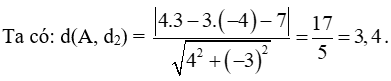Giải Toán 10 trang 86 Tập 2 Cánh diều

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 86 Tập 2 trong Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng Toán lớp 10 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 86.

Giải Toán 10 trang 86 Tập 2 Cánh diều

Bài 1 trang 86 Toán lớp 10 Tập 2: Xét vị trí tương đối của mỗi cặp đường thẳng sau:

Lời giải:

a) Tọa độ giao điểm của đường thẳng d₁ và d₂ là nghiệm của hệ phương trình

Hệ trên tương đương với

Hệ có nghiệm duy nhất (x; y) = $\left(\frac{9}{7};\frac{4}{7}\right)$.

Vậy hai đường thẳng d₁ và d₂ có 1 điểm chung, tức là chúng cắt nhau tại giao điểm $\left(\frac{9}{7};\frac{4}{7}\right).$

b) Tọa độ giao điểm của đường thẳng d₃ và d₄ là nghiệm của hệ phương trình

Hệ trên tương đương với

Do đó, hệ vô nghiệm.

Vậy hai đường thẳng d₃ và d₄ không có điểm chung, tức là d₃ // d₄.

c) Đường thẳng d₅ có một vectơ pháp tuyến là $\overrightarrow{n_5}=\left(4;2\right)$, do đó nó có một vectơ chỉ phương là $\overrightarrow{u_5}=\left(2;-4\right)$.

Đường thẳng d₆ có một vectơ chỉ phương là $\overrightarrow{u_6}=\left(1;-2\right)$.

Ta có: $\overrightarrow{u_5}=2\overrightarrow{u_6}$ nên hai vectơ $\overrightarrow{u_5},\overrightarrow{u_6}$ cùng phương.

Ứng với t = 0, thay vào phương trình d₆, ta được

Do đó, điểm M$\left(-\frac{1}{2};\frac{5}{2}\right)$ thuộc đường thẳng d₆.

Thay tọa độ điểm M vào phương trình đường thẳng d₅, ta được: $4.\left(-\frac{1}{2}\right)+2.\frac{5}{2}-3=0$⇔ 0 = 0.

Khi đó điểm M thuộc đường thẳng d₅.

Vậy hai đường thẳng d₅ và d₆ trùng nhau.

Bài 2 trang 86 Toán lớp 10 Tập 2: Tính số đo góc giữa hai đường thẳng d1: 2x – y + 5 = 0 và d2: x – 3y + 3 = 0.

Lời giải:

Đường thẳng d₁ có vectơ pháp tuyến là $\overrightarrow{n_1}=\left(2;-1\right)$.

Đường thẳng d₂ có vectơ pháp tuyến là $\overrightarrow{n_2}=\left(1;-3\right)$.

Vậy (d₁, d₂) = 45°.

Bài 3 trang 86 Toán lớp 10 Tập 2: Tính khoảng cách từ một điểm đến một đường thẳng trong mỗi trường hợp sau:

Lời giải:

a) Khoảng cách từ A đến ∆₁ là:

b) Đường thẳng ∆₂ có một vectơ chỉ phương là $\overrightarrow{u_2}=\left(1;-2\right)$, do đó nó có một vectơ pháp tuyến là $\overrightarrow{n_2}=\left(2;1\right)$.

Ứng với t = 0 thay vào phương trình ∆₂ ta được:

Do đó điểm H(– 2; 1) thuộc ∆₂.

Khi đó phương trình tổng quát của đường thẳng ∆₂ là 2(x + 2) + 1(y – 1) = 0 hay 2x + y + 3 = 0.

Do đó, khoảng cách từ B đến ∆₂ là:

Bài 4 trang 86 Toán lớp 10 Tập 2: Với giá trị nào của tham số m thì hai đường thẳng sau đây vuông góc?

Δ₁: mx – y + 1 = 0 và Δ₂: 2x – y + 3 = 0.

Lời giải:

Đường thẳng ∆₁ có một vectơ pháp tuyến là $\overrightarrow{n_1}=\left(m;-1\right)$.

Đường thẳng ∆₂ có một vectơ pháp tuyến là $\overrightarrow{n_2}=\left(2;-1\right)$.

Ta có: ∆₁ ⊥ ∆₂ ⇔ $\iff \overrightarrow{n_1}\perp \overrightarrow{n_2}\iff \overrightarrow{n_1}.\overrightarrow{n_2}=0$$\iff$m . 2 + (– 1) . (– 1) = 0 ⇔ m = $-\frac{1}{2}$.

Vậy m = $-\frac{1}{2}$ thì hai đường thẳng ∆₁ và ∆₂ vuông góc với nhau.

Bài 5 trang 86 Toán lớp 10 Tập 2: Cho ba điểm A(2; – 1), B(1; 2) và C(4; – 2). Tính số đo góc BAC và góc giữa hai đường thẳng AB, AC.

Lời giải:

Ta có: $\overrightarrow{AB}=\left(-1;3\right),\overrightarrow{AC}=\left(2;-1\right)$.

Do đó, $\widehat{BAC}=135°$.

Do đó, (AB, AC) = 45°.

Bài 6 trang 86 Toán lớp 10 Tập 2: Cho ba điểm A(2; 4), B(– 1; 2) và C(3; – 1). Viết phương trình đường thẳng đi qua B đồng thời cách đều A và C.

Lời giải:

Gọi d là đường thẳng đi qua B và cách đều A và C.

Do d đi qua B(– 1; 2) nên phương trình đường thẳng d có dạng a(x + 1) + b(y – 2) = 0 hay ax + by + a – 2b = 0 (với a và b không đồng thời bằng 0).

Vì d cách đều A và C nên d(A, d) = d(C, d).

Trường hợp 1: 3a + 2b = 4a – 3b ⇔ a = 5b.

Chọn b = 1, a = 5 . 1 = 5, ta có phương trình đường thẳng d là 5x + y + 5 – 2 = 0 hay 5x + y + 3 = 0.

Trường hợp 2: 3a + 2b = – (4a – 3b) ⇔ 7a = b.

Chọn a = 1, b = 7 . 1 = 7, ta có phương trình đường thẳng d là x + 7y + 1 – 2 . 7 = 0 hay x + 7y – 13 = 0.

Vậy phương trình đường thẳng cần lập là 5x + y + 3 = 0 hoặc x + 7y – 13 = 0.

Lưu ý: Do vectơ $\overrightarrow{n}=\left(a;b\right)$ là vectơ pháp tuyến của đường thẳng d, mà một đường thẳng có vô số vectơ pháp tuyến, nên khi ta có hệ thức liên hệ giữa a và b thì ta có thể chọn a rồi suy ra b hoặc ngược lại.

Bài 7 trang 86 Toán lớp 10 Tập 2:

a) Tính côsin góc giữa hai đường đi của hai tàu A và B.

b) Sau bao lâu kể từ thời điểm xuất phát hai tàu gần nhau nhất?

c) Nếu tàu A đứng yên ở vị trí ban đầu, tàu B chạy thì khoảng cách ngắn nhất giữa hai tàu bằng bao nhiêu?

Lời giải:

a) Giả sử đường đi của tàu A là d₁, khi đó phương trình d₁:

Giả sử đường đi của tàu B là d₂, vị trí của tàu B có tọa độ là (4 – 30t; 3 – 40t) nên phương trình d₂:

Đường thẳng d₁ có vectơ chỉ phương là $\overrightarrow{u_1}=\left(-33;25\right)$.

Đường thẳng d₂ có vectơ chỉ phương là $\overrightarrow{u_2}=\left(-30;-40\right)$.

Vậy côsin góc giữa hai đường đi của hai tàu A và B là $\frac{1}{5\sqrt{1714}}$.

b) Đường thẳng d₁ đi qua điểm A(3; – 4) và có một vectơ pháp tuyến là $\overrightarrow{n_1}=\left(25;33\right)$.

Do đó phương trình tổng quát của d₁ là 25(x – 3) + 33(y + 4) = 0 hay 25x + 33y + 57 = 0.

Đường thẳng d₂ đi qua điểm B(4; 3) và có một vectơ pháp tuyến là $\overrightarrow{n_2}=\left(4;-3\right)$.

Do đó phương trình tổng quát của d₂ là 4(x – 4) – 3(y – 3) = 0 hay 4x – 3y – 7 = 0.

Tọa độ giao điểm của hai đường thẳng d₁ và d₂ là nghiệm của hệ phương trình

Do đó hai đường thẳng d₁ và d₂ cắt nhau tại điểm có tọa độ $\left(\frac{20}{69};-\frac{403}{207}\right)$.

Khi đó hai tàu A và tàu B gần nhau nhất khi hai tàu ở vị trí tọa độ $\left(\frac{20}{69};-\frac{403}{207}\right)$.

Thay tọa độ $\left(\frac{20}{69};-\frac{403}{207}\right)$ vào phương trình tham số d₁ ta được:

Vậy sau $\frac{17}{207}$ giờ kể từ thời điểm xuất phát thì hai tàu gần nhau nhất.

c) Vì tàu A đứng yên ở vị trí ban đầu nên thời gian tàu A chạy là t = 0, do đó tàu A đứng ở vị trí A(3; – 4).

Khi đó khoảng cách ngắn nhất giữa hai tàu chính là khoảng cách từ điểm A đến đường đi của tàu B chính là đường thẳng d₂: 4x – 3y – 7 = 0.

Vậy nếu tàu A đứng yên ở vị trí ban đầu, tàu B chạy thì khoảng cách ngắn nhất giữa hai tàu bằng 3,4 km.

Lời giải bài tập Toán lớp 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng Cánh diều hay khác:

• Giải Toán 10 trang 81 Tập 2
• Giải Toán 10 trang 82 Tập 2
• Giải Toán 10 trang 83 Tập 2
• Giải Toán 10 trang 84 Tập 2
• Giải Toán 10 trang 85 Tập 2