Bài 4 trang 78 Toán 10 Tập 1 Chân trời sáng tạo

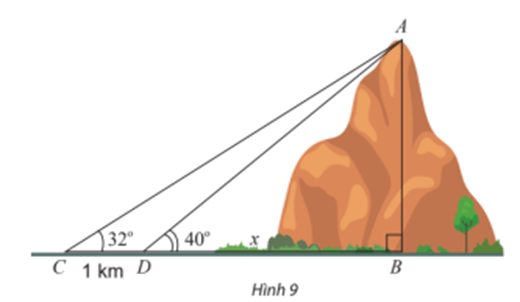
Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là 32° và 40° (Hình 9).

Giải Toán lớp 10 Bài 3: Giải tam giác và ứng dụng thực tế

Bài 4 trang 78 Toán lớp 10 Tập 1: Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là 32° và 40° (Hình 9).

Lời giải:

Đặt BD = x km, khi đó ta có CB = BD + CD = x + 1.

Trong tam giác ABC vuông tại B ta có:

$\tan \widehat{ACB}=\tan {32}^o=\frac{AB}{CB}=\frac{AB}{x+1}\Rightarrow AB=(x+1)\tan {32}^o=x\tan {32}^o+\tan {32}^o$     (1)

Trong tam giác ABD vuông tại B ta có:

 $\tan \widehat{ADB}=\tan {40}^o=\frac{AB}{BD}=\frac{AB}{x}\Rightarrow AB=x\tan {40}^o$   (2)

Từ (1) và (2) suy ra: $x\tan {32}^o+\tan {32}^o=x\tan {40}^o\Rightarrow x=\frac{\tan {32}^o}{\tan {40}^o-\tan {32}^o}\approx 2,92$.

Suy ra AB = x.tan40° ≈ 2,92.tan40° ≈ 2,45 km.

Vậy chiều cao AB của một ngọn núi khoảng 2,45 km.

Lời giải bài tập Toán 10 Bài 3: Giải tam giác và ứng dụng thực tế hay, chi tiết khác:

• Hoạt động khởi động trang 74 Toán lớp 10 Tập 1: Với số liệu đo được từ một bên bờ sông như hình vẽ bên, bạn hãy giúp nhân viên đo đạc tính khoảng cách giữa hai cái cây bên kia bờ sông ....

• Thực hành trang 75 Toán lớp 10 Tập 1: Giải tam giác ABC trong các trường hợp sau: a = 17,4; $\widehat{B}={44}^{o}30\text{'};\widehat{C}={64}^o$ ....

• Vận dụng 1 trang 76 Toán lớp 10 Tập 1: Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với vận tốc 450 km/h theo hướng tây ....

• Vận dụng 2 trang 77 Toán lớp 10 Tập 1: Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên ....

• Bài 1 trang 77 Toán lớp 10 Tập 1: Giải tam giác ABC trong các trường hợp sau: AB = 14, AC = 23, $\widehat{A}={125}^o$ ....

• Bài 2 trang 77 Toán lớp 10 Tập 1: Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8 km ....

• Bài 3 trang 77 Toán lớp 10 Tập 1: Một người đứng cách thân một cái quạt gió 16 m và nhìn thấy tâm của cánh quạt với góc nâng 56,5° (Hình 8). Tính khoảng cách từ tâm của cánh quạt đến mặt đất ....

• Bài 5 trang 78 Toán lớp 10 Tập 1: Hai người quan sát khinh khí cầu tại hai địa điểm P và Q nằm ở sườn đồi nghiêng 32° so với phương ngang, cách nhau 60 m (Hình 10). Người quan sát tại P xác định góc nâng của khinh khí cầu là 62° ....

• Bài 6 trang 78 Toán lớp 10 Tập 1: Một người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt đất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là 43° ....