Giải Toán 10 trang 60 Tập 2 Chân trời sáng tạo

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 60 Tập 2 trong Bài 3: Đường tròn trong mặt phẳng toạ độ Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 60.

Giải Toán 10 trang 60 Tập 2 Chân trời sáng tạo

Thực hành 1 trang 60 Toán lớp 10 Tập 2: Viết phương trình đường tròn (C) trong các trường hợp sau:

a) (C) có tâm O(0; 0), bán kính R = 4;

b) (C) có tâm I(2; -2), bán kính R = 8;

c) (C) đi qua ba điểm A(1; 4), B(0; 1), C(4; 3).

Lời giải:

a) Phương trình đường tròn (C) có tâm O(0; 0), bán kính R = 4 là:

(x – 0)² + (y – 0)² = 4²

⇔ x² + y² = 16.

Vậy phương trình đường tròn (C) cần tìm là x² + y² = 16.

b) Phương trình đường tròn (C) có tâm I(2; -2), bán kính R = 8 là:

(x – 2)² + (y + 2)² = 8²

Vậy phương trình đường tròn (C) cần tìm là (x – 2)² + (y + 2)² = 8².

c) Gọi I(a; b) là tâm của đường tròn (C), khi đó ta có:

$\overrightarrow{AI}\left(a-1;b-4\right)$ ⇒ AI = $\sqrt{{\left(a-1\right)}^2+{\left(b-4\right)}^2}$;

$\overrightarrow{BI}\left(a;b-1\right)$ ⇒ BI = $\sqrt{a^2+{\left(b-1\right)}^2}$;

$\overrightarrow{CI}\left(a-4;b-3\right)$ ⇒ CI = $\sqrt{{\left(a-4\right)}^2+{\left(b-3\right)}^2}$.

Vì đường tròn (C) đi qua ba điểm A, B, C nên ta có:

AI = BI = CI = R

Khi đó ta có hệ phương trình sau:

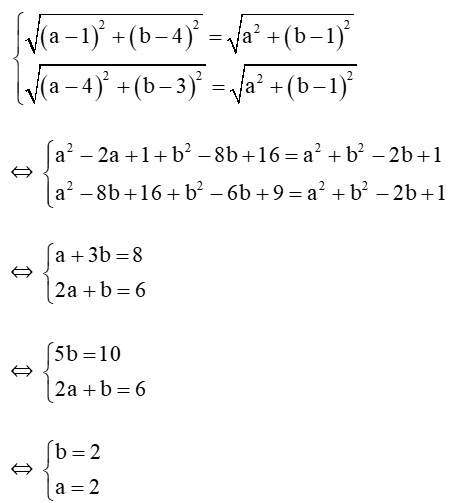
Suy ra tâm I(2; 2)

Bán kính của đường tròn (C) là: R = $\sqrt{a^2+{\left(b-1\right)}^2}$= $\sqrt{2^2+{\left(2-1\right)}^2}=\sqrt{5}$.

Phương trình đường tròn (C) là:

(x – 2)² + (y – 2)² = ${\left(\sqrt{5}\right)}^2$

⇔ (x – 2)² + (y – 2)² = 5.

Vậy phương trình đường tròn (C) là (x – 2)² + (y – 2)² = 5.

Lời giải bài tập Toán lớp 10 Bài 3: Đường tròn trong mặt phẳng toạ độ Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 59 Tập 2

• Giải Toán 10 trang 61 Tập 2

• Giải Toán 10 trang 62 Tập 2

• Giải Toán 10 trang 63 Tập 2