Giải Toán 10 trang 61 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 61 Tập 2 trong Bài 3: Đường tròn trong mặt phẳng toạ độ Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 61.

Giải Toán 10 trang 61 Tập 2 Chân trời sáng tạo

Thực hành 2 trang 61 Toán lớp 10 Tập 2: Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó.

a) x² + y² – 2x – 4y – 20 = 0;

b) (x + 5)² + (y + 1)² = 121;

c) x² + y² – 4x – 8y + 5 = 0;

d) 2x² + 2y² + 6x + 8y – 2 = 0.

Lời giải:

a) Phương trình đã cho có dạng x² + y² – 2ax – 2by + c = 0 với a = 1, b = 2 và c = -20.

Ta có: a² + b² – c = 1² + 2² – (-20) = 25 > 0.

Vậy đây là phương trình đường tròn có tâm là I(1; 2) và bán kính R = $\sqrt{25}$ = 5.

b) Phương trình đã cho có dạng tổng quát của phương trình đường tròn.

Vậy đây là phương trình đường tròn có tâm là I(-5; -1) và bán kính R = $\sqrt{121}$ = 11.

c) Phương trình đã cho có dạng x² + y² – 2ax – 2by + c = 0 với a = 2, b = 4 và c = 5.

Ta có: a² + b² – c = 2² + 4² – 5 = 15 > 0.

Vậy đây là phương trình đường tròn có tâm là I(2; 4) và bán kính R = $\sqrt{15}$.

d) 2x² + 2y² + 6x + 8y – 2 = 0

⇔ x² + y² + 3x + 4y – 1 = 0 (chia cả hai vế cho 2)

Phương trình đã cho có dạng x² + y² – 2ax – 2by + c = 0 với a = $-\frac{3}{2}$, b = -2 và c = -1.

Ta có: a² + b² – c = ${\left(-\frac{3}{2}\right)}^2+{\left(-2\right)}^2-\left(-1\right)=\frac{29}{4}$ > 0.

Vậy đây là phương trình đường tròn có tâm là I$\left(-\frac{3}{2};-2\right)$ và bán kính R = $\sqrt{\frac{29}{4}}$.

Vận dụng 1 trang 61 Toán lớp 10 Tập 2: Theo dữ kiện đã cho trong hoạt động của bài học, viết phương trình đường tròn biểu diễn tập hợp các điểm xa nhất mà vòi nước có thể phun tới.

Lời giải:

Tập hợp các điểm xa nhất mà vòi này có thể phun tới là đường tròn có tâm là tâm một vòi phun.

Phương trình biểu diến tập hợp các điểm xa nhất mà vòi này có thể phun tới là phương trình đường tròn có tâm là điểm có tọa độ (30; 40) và bán kính là 50 có dạng:

(x – 30)² + (y – 40)² = 50².

Vận dụng 2 trang 61 Toán lớp 10 Tập 2: Một sân khấu đã được thiết lập một hệ trục tọa độ để đạo diễn có thể sắp đặt ánh sáng và xác định vị trí của các diễn viên. Chi biết một đèn chiếu đang rọi trên sân khấu một vùng sáng bên trong đường tròn (C) có phương trình (x – 13)² + (y – 4)² = 16.

a) Tìm tọa độ tâm và bán kính của đường tròn (C).

b) Cho biết tọa độ trên sân khấu của ba diễn viên A, B, C như sau: A(11; 4), B(8; 5), C(15; 5). Diễn viên nào đang được đèn chiếu sáng?

Lời giải:

a) Xét phương trình đường tròn (C): (x – 13)² + (y – 4)² = 16.

Đường tròn này có tâm I(13; 4) và bán kính R = $\sqrt{16}$ = 4.

Vậy tâm của đường tròn (C) là I(13; 4) và bán kính R = 4.

b) Ta có: $\overrightarrow{IA}$ = (-2; 0) ⇒ IA = $\sqrt{{\left(-2\right)}^2+0^2}$ = 2;

$\overrightarrow{IB}$ = (-5; 1) ⇒ IB = $\sqrt{{\left(-5\right)}^2+1^2}=\sqrt{26}$;

$\overrightarrow{IC}$ = (2; 1) ⇒ IA = $\sqrt{2^2+1^2}=\sqrt{5}$;

Biết một đèn chiếu đang rọi trên sân khấu một vùng sáng bên trong đường tròn (C). Diễn viên được chiếu sáng nghĩa là phải nằm trên đường tròn hoặc trong đường tròn (C). Hay chính là khoảng cách từ các điểm A, B, C đến tâm I của đường tròn (C) phải nhỏ hơn hoặc bằng bán kính R của (C).

Vì 2 < 4 nên IA < R hay A nằm trong đường tròn (C). Do đó diễn viễn A được đèn chiếu sáng.

Vì $\sqrt{26}>\sqrt{16}=4$ nên IB > R hay B nằm ngoài đường tròn (C). Do đó diễn viên B không được đèn chiếu sáng.

Vì $\sqrt{5}<\sqrt{16}=4$ nên IC < R hay C nằm trong đường tròn (C). Do đó diễn viên C được đèn chiếu sáng.

Vậy diễn viên A và C được đèn chiếu sáng, diễn viên B không được đèn chiếu sáng.

Hoạt động khám phá 2 trang 61 Toán lớp 10 Tập 2: Cho điểm M(x₀; y₀) nằm trên đường tròn (C) tâm I(a; b) và cho điểm M(x; y) tùy ý trong mặt phẳng Oxy. Gọi ∆ là tiếp tuyến của (C) tại M₀.

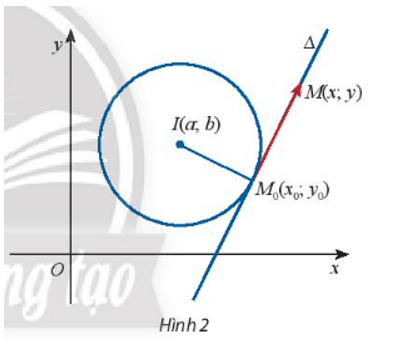
a) Viết tọa độ của hai vectơ $\overrightarrow{M_{0}M}$ và $\overrightarrow{M_{0}I}$.

b) Viết biểu thức tọa độ của tích vô hướng của hai vectơ $\overrightarrow{M_{0}M}$ và $\overrightarrow{M_{0}I}$.

c) Hệ thức $\overrightarrow{M_{0}M}.\overrightarrow{M_{0}I}=0$ cho ta phương trình của đường thẳng nào?

Lời giải:

a) Biểu thức tọa độ của hai vectơ $\overrightarrow{M_{0}M}$ và $\overrightarrow{M_{0}I}$ là:

$\overrightarrow{M_{0}M}$ = (x – x₀; y – y₀);

$\overrightarrow{M_{0}I}$ = (a – x₀; b – y₀).

b) Biểu thức tọa độ tích vô hướng của hai vectơ $\overrightarrow{M_{0}M}$ và $\overrightarrow{M_{0}I}$ là:

$\overrightarrow{M_{0}M}.\overrightarrow{M_{0}I}$ = (x – x₀)(a – x₀) + (y – y₀).(b – y₀).

c) Ta có hệ thức $\overrightarrow{M_{0}M}.\overrightarrow{M_{0}I}=0$

⇔ (x – x₀)(a – x₀) + (y – y₀).(b – y₀) = 0 (*)

Vì ∆ là tiếp tuyến của đường tròn (C) nên ∆ ⊥ IM₀. Do đó phương trình đường thẳng ∆ nhận vectơ $\overrightarrow{M_{0}M}$ làm VTPT và đi qua điểm M₀(x₀; y₀) là:

(a – x₀)(x – x₀) + (b – y₀)(y – y₀) = 0

Và đây cũng chính là phương trình (*).

Vậy hệ thức $\overrightarrow{M_{0}M}.\overrightarrow{M_{0}I}=0$ là phương trình của đường thẳng ∆ là tiếp tuyến của đường tròn (C).

Lời giải bài tập Toán lớp 10 Bài 3: Đường tròn trong mặt phẳng toạ độ Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 59 Tập 2

• Giải Toán 10 trang 60 Tập 2

• Giải Toán 10 trang 62 Tập 2

• Giải Toán 10 trang 63 Tập 2