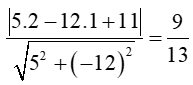Giải Toán 10 trang 62 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 62 Tập 2 trong Bài 3: Đường tròn trong mặt phẳng toạ độ Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 62.

Giải Toán 10 trang 62 Tập 2 Chân trời sáng tạo

Thực hành 3 trang 62 Toán lớp 10 Tập 2: Viết phương trình tiếp tuyến của đường tròn (C): x² + y² – 2x – 4y – 20 = 0 tại điểm A(4; 6).

Lời giải:

Xét phương trình đường tròn (C): x² + y² – 2x – 4y – 20 = 0

⇔ x² – 2x + 1 + y² – 4y + 4 = 25

⇔ (x – 1)² + (y – 2)² = 5²

Suy ra phương trình đường tròn (C) có tâm I(1; 2) và bán kính R = 5.

Phương trình tiếp tuyến của đường tròn (C) tại điểm A(4; 6) là:

(1 – 4)(x – 4) + (2 – 6)(y – 6) = 0

⇔ - 3(x – 4) – 4(y – 6) = 0

⇔ 3x + 4y – 36 = 0

Vậy phương trình tiếp tuyến của đường tròn (C) tại điểm A(4; 5) là: 3x + 4y – 36 = 0.

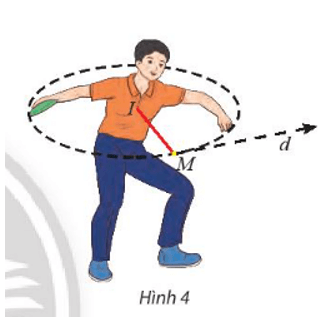
Vận dụng 3 trang 62 Toán lớp 10 Tập 2: Một vận động viên ném đĩa đã vung đĩa theo một đường tròn (C) có phương trình:

(x – 1)² + (y – 1)² = $\frac{169}{144}$

Khi người đó vung đĩa đến vị trí điểm M$\left(\frac{17}{12};2\right)$ thì buông đĩa (Hình 4). Viết phương trình tiếp tuyến của đường tròn (C) tại điểm M.

Lời giải:

Phương trình đường tròn (C) có tâm I(1; 1).

Khi đó $\overrightarrow{IM}\left(\frac{5}{12};1\right)$

Phương trình tiếp tuyến của đường tròn (C) tại điểm M nhận $\overrightarrow{IM}\left(\frac{5}{12};1\right)$ làm VTPT là:

$\frac{5}{12}\left(x-\frac{17}{12}\right)+y-2=0$

⇔ $5x+12y-\frac{373}{12}=0$

Vậy phương trình tiếp tuyến của đường tròn (C) tại điểm M là $5x+12y-\frac{373}{12}=0$.

Bài 1 trang 62 Toán lớp 10 Tập 2: Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó.

a) x² + y² – 6x – 8y + 21 = 0;

b) x² + y² – 2x + 4y + 2 = 0;

c) x² + y² – 3x + 2y + 7 = 0;

d) 2x² + 2y² + x + y – 1 = 0.

Lời giải:

a) Phương trình đã cho có dạng x² + y² – 2ax – 2by + c = 0 với a = 3, b = 4, c = 21.

Ta có: a² + b² – c = 3² + 4² – 21 = 4 > 0.

Vậy phương trình đã cho là phương trình đường tròn có tâm I(3; 4) và bán kính R = $\sqrt{4}$ = 2.

b) Phương trình đã cho có dạng x² + y² – 2ax – 2by + c = 0 với a = 1, b = - 2, c = 2.

Ta có: a² + b² – c = 1² + (-2)² – 2 = 3 > 0.

Vậy phương trình đã cho là phương trình đường tròn có tâm I(1; -2) và bán kính R = $\sqrt{3}$.

c) Phương trình đã cho có dạng x² + y² – 2ax – 2by + c = 0 với a = $\frac{3}{2}$, b = -1, c = 7.

Ta có: a² + b² – c = ${\left(\frac{3}{2}\right)}^2$ + (-1)² – 7 = $-\frac{15}{4}$ < 0.

Vậy phương trình đã cho không là phương trình đường tròn.

d) 2x² + 2y² + x + y – 1 = 0

⇔ x² + y² + $\frac{1}{2}$x + $\frac{1}{2}$y – $\frac{1}{2}$ = 0

Phương trình đã cho có dạng x² + y² – 2ax – 2by + c = 0 với a = $-\frac{1}{4}$, b = $-\frac{1}{4}$, c = $-\frac{1}{2}$.

Ta có: a² + b² – c = ${\left(-\frac{1}{4}\right)}^2+{\left(-\frac{1}{4}\right)}^2-\left(-\frac{1}{2}\right)=\frac{10}{16}=\frac{5}{8}$ > 0.

Vậy phương trình đã cho là phương trình đường tròn có tâm $I\left(-\frac{1}{4};\frac{1}{4}\right)$ và bán kính $R=\sqrt{\frac{5}{8}}$.

Bài 2 trang 62 Toán lớp 10 Tập 2: Lập phương trình đường tròn (C) trong các trường hợp sau:

a) (C) có tâm I(1; 5) có bán kính r = 4;

b) (C) có đường kính MN với M(3; -1) và N(9; 3);

c) (C) có tâm I(2; 1) và tiếp xúc với đường thẳng 5x – 12y + 11 = 0;

d) (C) có tâm A(1; -2) và đi qua điểm B(4; -5).

Lời giải:

a) Phương trình đường tròn (C) có tâm I(1; 5) và bán kính r = 4 là:

(x – 1)² + (y – 5)² = 4²

⇔ (x – 1)² + (y – 5)² = 16.

Vậy phương trình đường tròn (C) có tâm I(1; 5) và bán kính r = 4 là (x – 1)² + (y – 5)² = 16.

b) Tâm I của đường tròn (C) là trung điểm của đoạn thẳng MN.

Khi đó tọa độ tâm I của đường tròn (C) là: I = $\left(\frac{9+3}{2};\frac{-1+3}{2}\right)=$(6; 1).

Ta có: $\overrightarrow{MN}$ = (6; 4) ⇒ MN = $\sqrt{6^2+4^2}=\sqrt{52}$

Vì MN là đường kính của đường tròn (C) nên bán kính của (C) bằng $\frac{MN}{2}=\frac{\sqrt{52}}{2}$.

Phương trình đường tròn (C) có tâm I(6; 1) và bán kính R = $\frac{\sqrt{52}}{2}$ là:

(x – 6)² + (y – 1)² = ${\left(\frac{\sqrt{52}}{2}\right)}^2$

⇔ (x – 6)² + (y – 1)² = 13.

Vậy phương trình đường tròn (C) cần tìm là (x – 6)² + (y – 1)² = 13.

c) Bán kính của đường tròn (C) là khoảng cách từ điểm I đến đường thẳng 5x – 12y + 11 = 0 là:

Phương trình đường tròn (C) có tâm I(2; 1) và bán kính là R = $\frac{9}{13}$ là:

(x – 2)² + (y – 1)² = ${\left(\frac{9}{13}\right)}^2$

⇔ (x – 2)² + (y – 1)² = $\frac{81}{169}$

Vậy phương trình đường tròn (C) là (x – 2)² + (y – 1)² = $\frac{81}{169}$.

d) Bán kính của đường tròn (C) chính là độ dài đoạn thẳng AB.

Ta có $\overrightarrow{AB}$ = (3; -3) ⇒ AB = $\sqrt{3^2+{\left(-3\right)}^2}=3\sqrt{2}$.

Khi đó R = AB = 3$\sqrt{2}$

Phương trình đường tròn tâm A(1; -2) bán kính R = 3$\sqrt{2}$ là:

(x – 1)² + (y + 2)² = ${\left(3\sqrt{2}\right)}^2$

⇔ (x – 1)² + (y + 2)² = 18.

Vậy phương trình đường tròn cần tìm là (C): (x – 1)² + (y + 2)² = 18.

Bài 3 trang 62 Toán lớp 10 Tập 2: Lập phương trình đường tròn ngoại tiếp tam giác có tọa độ các đỉnh là:

a) M(2; 5), N(1; 2), P(5; 4);

b) A(0; 6), B(7; 7), C(8; 0).

Lời giải:

a) Gọi (C) là đường tròn ngoại tiếp tam giác MNP, có tâm là I(a; b) và bán kính R.

Khi đó:

$\overrightarrow{MI}$ = (a – 2; b – 5) ⇒ MI = $\sqrt{{\left(a-2\right)}^2+{\left(b-5\right)}^2}$

$\overrightarrow{NI}$ = (a – 1; b – 2) ⇒ NI = $\sqrt{{\left(a-1\right)}^2+{\left(b-2\right)}^2}$

$\overrightarrow{PI}$ = (a – 5; b – 4) ⇒ PI = $\sqrt{{\left(a-5\right)}^2+{\left(b-4\right)}^2}$

Ta có: MI = NI = PI = R nên ta có hệ phương trình:

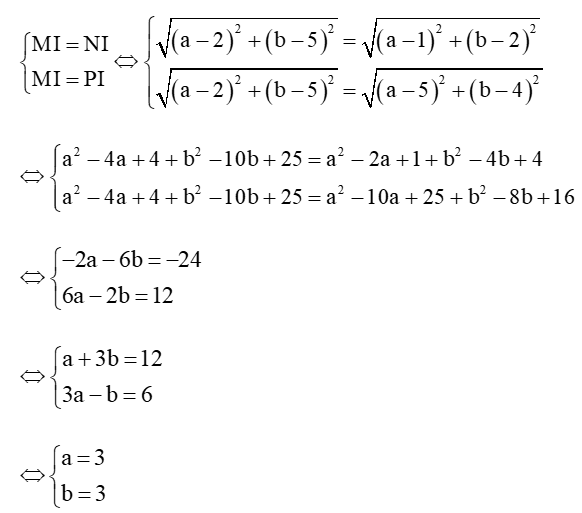
⇒ I(3; 3) và MI = $\sqrt{{\left(3-2\right)}^2+{\left(3-5\right)}^2}=\sqrt{5}$.

Do đó phương trình đường tròn ngoại tiếp tam giác MNP có tâm I(3; 3) và bán kính R = $\sqrt{5}$ là:

(x – 3)² + (y – 3)² = ${\left(\sqrt{5}\right)}^2$

⇔ (x – 3)² + (y – 3)² = 5.

Vậy phương trình đường tròn ngoại tiếp tam giác MNP là: (x – 3)² + (y – 3)² = 5.

b) Gọi (C) là đường tròn ngoại tiếp tam giác ABC, có tâm là I(a; b) và bán kính R.

Khi đó:

$\overrightarrow{AI}$ = (a ; b – 6) ⇒ AI = $\sqrt{a^2+{\left(b-6\right)}^2}$

$\overrightarrow{BI}$ = (a – 7; b – 7) ⇒ BI = $\sqrt{{\left(a-7\right)}^2+{\left(b-7\right)}^2}$

$\overrightarrow{CI}$ = (a – 8; b) ⇒ CI = $\sqrt{{\left(a-8\right)}^2+b^2}$

Ta có: AI = BI = CI = R nên ta có hệ phương trình:

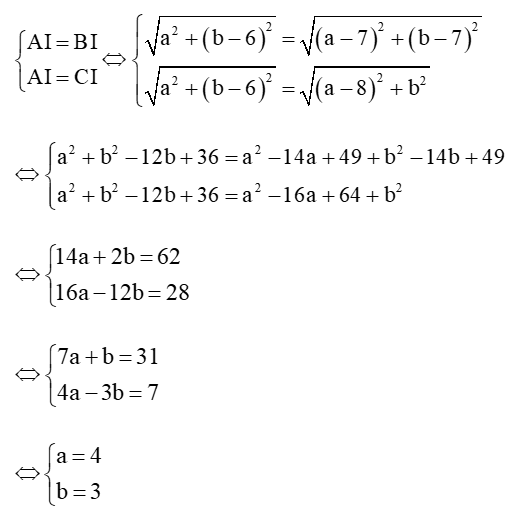
⇒ I(4; 3) và AI = $\sqrt{4^2+{\left(3-6\right)}^2}=\sqrt{25}=5$.

Do đó phương trình đường tròn ngoại tiếp tam giác ABC có tâm I(4; 3) và bán kính R = 5 là:

(x – 4)² + (y – 3)² = 5²

⇔ (x – 4)² + (y – 3)² = 25.

Vậy phương trình đường tròn ngoại tiếp tam giác ABC là: (x – 4)² + (y – 3)² = 25.

Bài 4 trang 62 Toán lớp 10 Tập 2: Lập phương trình đường tròn tiếp xúc với hai trục tọa độ Ox, Oy và đi qua điểm A(4; 2).

Lời giải:

Gọi đường tròn cần tìm là (C) có tâm là I(a; b) và bán kính R.

Vì đường tròn (C) tiếp xúc với hai trục tọa độ Ox, Oy và đi qua điểm A(4; 2) nên a = b và R = a.

Khi đó phương trình đường tròn (C) là:

(x – a)² + (y – a)² = a²

Ta lại có đường tròn (C) đi qua điểm A(4; 2) nên thay tọa độ điểm A vào phương trình đường tròn (C) ta được:

(4 – a)² + (2 – a)² = a²

⇔ 16 – 8a + a² + 4 – 4a + a² = a²

⇔ a² – 12a + 20 = 0

⇔ a = 10 hoặc a = 2

Với a = 10, phương trình đường tròn cần tìm là:

(x – 10)² + (y – 10)² = 10²

⇔ (x – 10)² + (y – 10)² = 100

Với a = 2, phương trình đường tròn cần tìm là:

(x – 2)² + (y – 2)² = 2²

⇔ (x – 2)² + (y – 2)² = 4

Vậy đường tròn (C) có hai phương trình thỏa mãn điều kiện đầu bài là:

(x – 10)² + (y – 10)² = 100 và (x – 2)² + (y – 2)² = 4.

Lời giải bài tập Toán lớp 10 Bài 3: Đường tròn trong mặt phẳng toạ độ Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 59 Tập 2

• Giải Toán 10 trang 60 Tập 2

• Giải Toán 10 trang 61 Tập 2

• Giải Toán 10 trang 63 Tập 2