Giải Toán 10 trang 8 Tập 2 Chân trời sáng tạo
Haylamdo biên soạn và sưu tầm giải Toán 10 trang 8 Tập 2 trong Bài 1: Dấu của tam thức bậc hai Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 8.
Giải Toán 10 trang 8 Tập 2 Chân trời sáng tạo
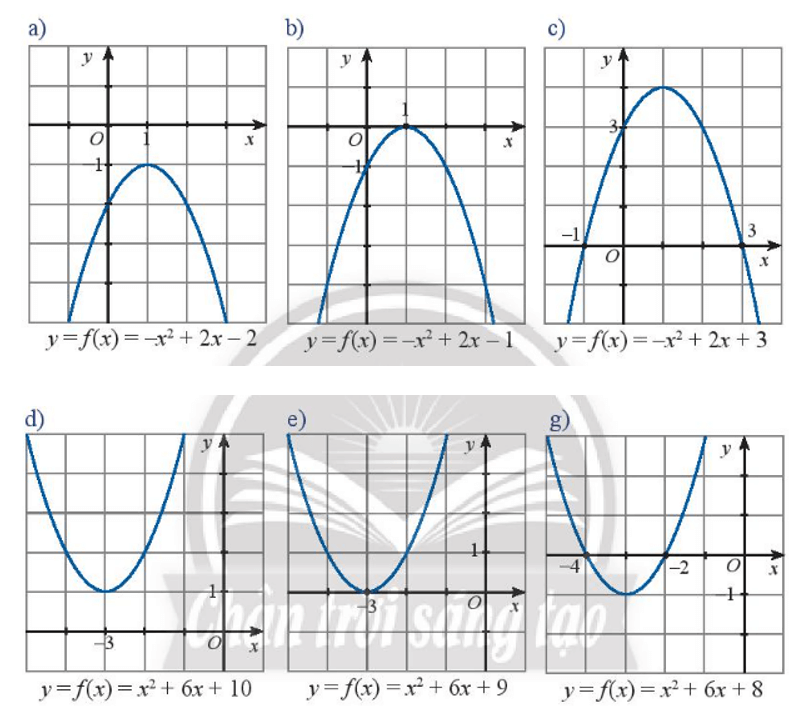
Hoạt động khám phá 2 trang 8 Toán lớp 10 Tập 2: Quan sát đồ thị của các hàm số bậc hai trong các hình dưới đây. Trong mỗi trường hợp hãy cho biết:
- Các nghiệm (nếu có) và dấu của biệt thức ∆.
- Các khoảng giá trị của x mà trên đó f(x) cùng dấu với hệ số của x2.
Lời giải:
a) Dựa vào hình vẽ ta thấy đồ thị hàm số không cắt trục hoành nên tam thức f(x) = - x2 + 2x – 2 vô nghiệm.
Ta có ∆ = 22 – 4(-1).(-2) = 4 – 8 = - 4 < 0.
Tam thức f(x) có hệ số a = -1 < 0.
Ta thấy toàn bộ đồ thị hàm số nằm phía dưới trục hoành nên f(x) < 0 với mọi x.
Suy ra f(x) cùng dấu với hệ số a với mọi x.
b) Dựa vào hình vẽ ta thấy đồ thị hàm số cắt trục hoành tại một điểm duy nhất có hoành độ x = 1 nên tam thức f(x) = - x2 + 2x – 1 có một nghiệm duy nhất x = 1.
Ta có ∆ = 22 – 4(-1).(-1) = 4 – 4 = 0.
Tam thức f(x) có hệ số a = -1 < 0.
Ta thấy với x ≠ 1 toàn bộ đồ thị hàm số nằm phía dưới trục hoành nên f(x) < 0 với x ≠ 1 và f(x) = 0 với x = 1.
Suy ra f(x) cùng dấu với hệ số a với x ≠ 1.
c) Dựa vào hình vẽ ta thấy đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt là x1 = - 1 và x2 = 3 nên tam thức f(x) = - x2 + 2x + 3 có hai nghiệm phân biệt x1 = - 1 và x2 = 3.
Ta có ∆ = 22 – 4.3.(-1) = 4 + 12 = 16 > 0.
Tam thức f(x) có hệ số a = -1 < 0.
Ta thấy với x < - 1 hoặc x > 3 thì đồ thị hàm số nằm phía dưới trục hoành, với -1 < x < 3 thì đồ thị hàm số nằm phía trên trục hoành hay f(x) < 0 với x < -1 hoặc x > 3; f(x) > 0 với -1 < x < 3 và f(x) = 0 tại x = -1 hoặc x = 3.
Suy ra f(x) cùng dấu với hệ số a với x < -1 hoặc x > 3.
d) Dựa vào hình vẽ ta thấy đồ thị hàm số không cắt trục hoành nên tam thức f(x) = x2 + 6x + 10 vô nghiệm.
Ta có ∆ = 62 – 4.1.10 = 36 – 40 = - 4 < 0.
Tam thức f(x) có hệ số a = 1 > 0.
Ta thấy toàn bộ đồ thị hàm số nằm phía trên trục hoành nên f(x) > 0 với mọi x.
Suy ra f(x) cùng dấu với hệ số a với mọi x.
e) Dựa vào hình vẽ ta thấy đồ thị hàm số cắt trục hoành tại một điểm duy nhất có hoành độ x = -3 nên tam thức f(x) = x2 + 6x + 9 có một nghiệm duy nhất x = -3.
Ta có ∆ = 62 – 4.1.9 = 36 – 36 = 0.
Tam thức f(x) có hệ số a = 1 > 0.
Ta thấy với x ≠ -3 toàn bộ đồ thị hàm số nằm phía trên trục hoành nên f(x) > 0 với x ≠ - 3 và f(x) = 0 với x = -3.
Suy ra f(x) cùng dấu với hệ số a với x ≠ -3.
g) Dựa vào hình vẽ ta thấy đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt là x1 = -4 và x2 = -2 nên tam thức f(x) = x2 + 6x + 8 có hai nghiệm phân biệt x1 = -4 và x2 = -2.
Ta có ∆ = 62 – 4.1.8 = 36 – 32 = 4 > 0.
Tam thức f(x) có hệ số a = 1 > 0.
Ta thấy với x < - 4 hoặc x > -2 thì đồ thị hàm số nằm phía trên trục hoành, với -4 < x < -2 thì đồ thị hàm số nằm phía dưới trục hoành hay f(x) > 0 với x < -4 hoặc x > 2; f(x) < 0 với -4 < x < -2 và f(x) = 0 tại x = -4 hoặc x = -2.
Suy ra f(x) cùng dấu với hệ số a với x < -4 hoặc x > -2.
Lời giải bài tập Toán lớp 10 Bài 1: Dấu của tam thức bậc hai Chân trời sáng tạo hay khác:

