Giải Toán 10 trang 9 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 9 Tập 2 trong Bài 1: Dấu của tam thức bậc hai Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 9.

Giải Toán 10 trang 9 Tập 2 Chân trời sáng tạo

Thực hành 3 trang 9 Toán lớp 10 Tập 2: Xét dấu của tam thức bậc hai sau:

a) f(x) = 2x² – 3x – 2;

b) g(x) = - x² + 2x – 3.

Lời giải:

a) Tam thức f(x) = 2x² – 3x – 2 có ∆ = (-3)² – 4.2.(-2) = 9 + 16 = 25 > 0. Do đó f(x) có hai nghiệm phân biệt x₁ = $-\frac{1}{2}$ và x₂ = 2 và a = 2 > 0.

Ta có bảng xét dấu sau:

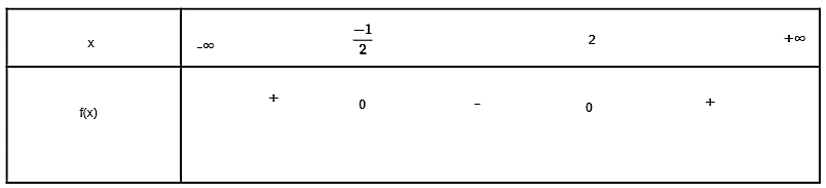
Dựa vào bảng xét dấu ta thấy f(x) âm trong khoảng $\left(-\frac{1}{2};2\right)$ và dương trong hai khoảng $\left(-\infty ;-\frac{1}{2}\right)$ và (2; +∞).

Vậy với x ∈ $\left(-\frac{1}{2};2\right)$ thì f(x) < 0 và x ∈ $\left(-\infty ;-\frac{1}{2}\right)$ hoặc x ∈ (2; +∞) thì f(x) > 0.

b) Tam thức g(x) = - x² + 2x – 3 có ∆ = 2² – 4.(-1).(-3) = 4 – 12 = - 8 < 0. Do đó g(x) vô nghiệm và a = -1 < 0.

Ta có bảng xét dấu sau:

Dựa vào bảng xét dấu ta thấy g(x) âm với mọi giá trị thực của x.

Vậy g(x) < 0 với mọi x ∈ ℝ.

Vận dụng trang 9 Toán lớp 10 Tập 2: Xét dấu tam thức bậc hai h(x) = -0,006x² + 1,2x – 30 trong bài toán khởi động và cho biết ở khoảng cách nào tính từ đầu cầu O thì vòm cầu: cao hơn mặt cầu, thấp hơn mặt cầu.

Lời giải:

Ta có h(x) = -0,006x² + 1,2x – 30 là tam thức bậc hai. h(x) có ∆ = 1,2² – 4.(-0,006).(-30) = 0,72 > 0. Do đó tam thức có hai nghiệm phân biệt là x₁ ≈ 170,7 và x₂ ≈ 29,3 và a = - 0,006 < 0.

Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy f(x) dương trong khoảng (29,3; 170,7) và âm trong hai khoảng (-∞; 29,3) và (170,7; +∞).

Kết hợp với điều kiện 0 ≤ x ≤ 200 thì f(x) dương khi x ∈ (29,3; 170,7) và f(x) âm khi x ∈ [0; 29,3) và (170,7; 200].

Vậy với giá trị của x ∈ (29,3; 170,7) thì vòm cầu cao hơn mặt cầu, với giá trị của x nằm trong hai khoảng (-∞; 29,3) và (170,7; +∞) thì vòm cầu thấp hơn mặt cầu.

Bài 1 trang 9 Toán lớp 10 Tập 2: Đa thức nào sau đây là tam thức bậc hai?

a) 4x² + 3x + 1;

b) x³ + 3x² – 1;

c) 2x² + 4x – 1.

Lời giải:

a) 4x² + 3x + 1 là tam thức bậc hai với a = 4, b = 3 và c = 1.

b) x³ + 3x² – 1 không là tam thức bậc hai vì bậc của đa thức là 3.

c) 2x² + 4x – 1 là tam thức bậc hai với a = 2, b = 4 và c = -1.

Bài 2 trang 9 Toán lớp 10 Tập 2: Xác định giá trị của m để đa thức sau là tam thức bậc hai.

a) (m + 1)x² + 2x + m;

b) mx³ + 2x² – x + m;

c) – 5x² + 2x – m + 1.

Lời giải:

a) Để đa thức (m + 1)x² + 2x + m là tam thức bậc hai thì hệ số của x² phải khác 0.

Suy ra m + 1 ≠ 0 ⇔ m ≠ - 1.

Vậy với m ≠ - 1 thì đa thức (m + 1)x² + 2x + m là tam thức bậc hai.

b) Để đa thức mx³ + 2x² – x + m là tam thức bậc hai thì bậc cao nhất của đa thức là 2 do đó hệ số của x³ phải bằng 0 hay m = 0.

Vậy với m = 0 thì đa thức mx³ + 2x² – x + m là tam thức bậc hai.

c) Để đa thức – 5x² + 2x – m + 1 thỏa mãn là tam thức bậc hai với mọi m.

Lời giải bài tập Toán lớp 10 Bài 1: Dấu của tam thức bậc hai Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 6 Tập 2

• Giải Toán 10 trang 7 Tập 2

• Giải Toán 10 trang 8 Tập 2

• Giải Toán 10 trang 10 Tập 2