Bạn Nam đứng dưới chân cầu vượt ba tầng ở nút giao ngã ba Huế, thuộc thành phố Đà nẵng để ngắm cầu vượt (H.6.13). Biết rằng trụ tháp cầu có dạng đường parabol, khoảng cách giữa hai chân trụ t

Hướng dẫn

Chọn hệ trục tọa độ Oxy sao cho một chân trụ tháp đặt tại gốc tọa độ, chân còn lại đặt trên tia Ox. Khi đó trụ tháp là một phần của đồ thị hàm số dạng y = ax² + bx.

Hướng dẫn giải

Chọn hệ trục tọa độ như hình vẽ:

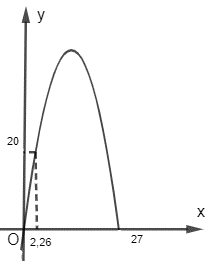
Một chân trụ cột tháp đặt tại gốc tọa độ nên điểm này có tọa độ (0; 0).

Khoảng cách giữa hai chân trụ tháp khoảng 27 m, và chân trụ còn lại đặt trên tia Ox, do đó điểm đặt chân trụ cột thứ 2 có tọa độ (27; 0).

Chiều cao của trụ tháp tính từ điểm trên mặt đất cách chân trụ tháp 2,26 m là 20 m, điều đó có nghĩa là điểm có tọa độ (2,26; 20) thuộc parabol như trên.

Do đó trụ tháp là một phần đồ thị của hàm số có dạng y = ax² + bx với a, b là các hằng số, a ≠ 0, đồ thị này đi qua các điểm (0; 0), (27; 0), (2,26; 20) như hình vẽ.

Vì đồ thị hàm số y = ax² + bx đi qua điểm có tọa độ (27; 0) nên ta có: 0 = a . 27² + b . 27

⇔ 729a + 27b = 0 ⇔ b = \( - \frac{{729a}}{{27}} = - 27a\)          (1).

Lại có đồ thị hàm số y = ax² + bx đi qua điểm có tọa độ (2,26; 20) nên ta có:

20 = a . 2,26² + b . 2,26    (2).

Thay (1) vào (2) ta được: 2,26² . a + (– 27a) . 2,26 = 20

⇔ – 55,9124a = 20

⇔ a ≈ – 0,358 (t/m)

Suy ra: b = – 27a ≈ (– 27) . (– 0,358) = 9,666.

Do đó ta có hàm số: y = – 0,358x² + 9,666x.

Tọa độ đỉnh: $\left\{\begin{array}{l}x=\frac{-b}{2a}\approx \frac{-\mathrm{9,666}}{2.\left(-\mathrm{0,358}\right)}=\mathrm{13,5}\\ y\approx \mathrm{65,2455}\end{array}\right.$

Suy ra đỉnh I(13,5; 65,2455).

Vậy độ cao của đỉnh trụ tháp cầu so với mặt đất khoảng 65,2455 m.