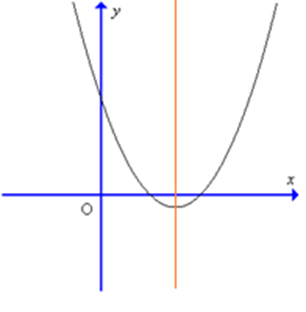
Cho hàm số y = f(x) có đồ thị như hình sau: Hàm số đồng biến trên khoảng
Câu hỏi:
Cho hàm số y = f(x) có đồ thị như hình sau:
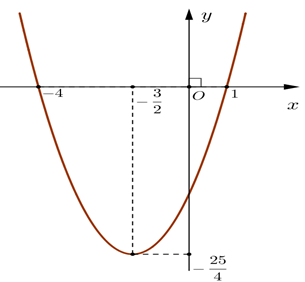
Hàm số đồng biến trên khoảng
A. \[\left( {--\infty {\rm{;}}--\frac{3}{2}} \right)\];
B. \[\left( {--\infty {\rm{;}}--\frac{{25}}{4}} \right)\];
C. \[\left( {--\frac{3}{2}; + \infty } \right)\];
D. \[\left( {--\frac{{{\rm{25}}}}{{\rm{4}}}; + \infty } \right)\].
Trả lời:
Đáp án đúng là: C
Đồ thị hàm số đi lên từ trái qua phải trên khoảng \[\left( {--\frac{{\rm{3}}}{{\rm{2}}}; + \infty } \right)\]nên hàm số đồng biến trên khoảng \[\left( {--\frac{3}{2}; + \infty } \right)\]