Cho hình bình hành ABCD. Vectơ nào dưới đây bằng vecto CD
Câu hỏi:
Cho hình bình hành ABCD. Vectơ nào dưới đây bằng \(\overrightarrow {CD} \).
A. \(\overrightarrow {DC} \);
B. \(\overrightarrow {AD} \);
C. \(\overrightarrow {CB} \);
D. \(\overrightarrow {BA} \).
Trả lời:
Đáp án đúng là D
Vì ABCD là hình bình hành nên AB // CD nên \(\overrightarrow {BA} \) và \(\overrightarrow {CD} \) cùng phương. Do đó \(\overrightarrow {BA} \) và \(\overrightarrow {CD} \) cùng hướng.
Mặt khác AB = CD (tính chất hình bình hành)
Suy ra \(\overrightarrow {BA} = \overrightarrow {CD} \).
Xem thêm bài tập trắc nghiệm Toán 10 KNTT có lời giải hay khác:
Câu 1:
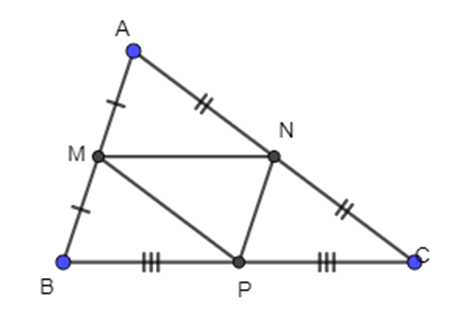
Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.
Phát biểu nào dưới đây là sai.
Xem lời giải »
Câu 2:
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
Xem lời giải »
Câu 3:
Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.
Xem lời giải »
Câu 4:
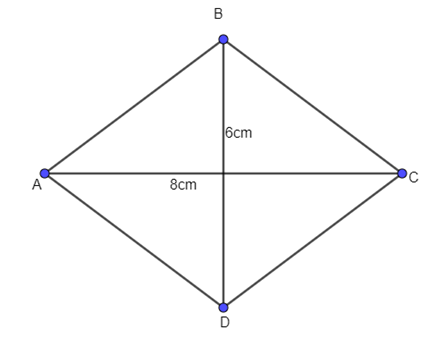
Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ \(\overrightarrow {AB} \).
Xem lời giải »
Câu 5:
Vectơ có điểm đầu là P điểm cuối là Q được kí hiệu là:
Xem lời giải »