Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập S gồm tất cả
Câu hỏi:
Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập S gồm tất cả các vecto khác , có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O}. Hãy chia tập S thành các nhóm sao cho hai vecto thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.
Trả lời:
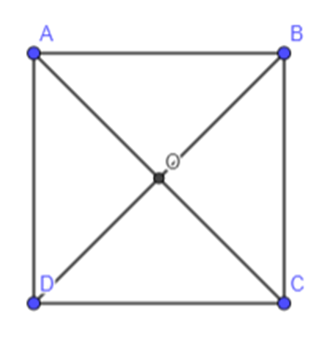
Các vecto khác , có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O} là:
Khi đó:
Hai vecto bằng nhau trong tập hợp S là:
Khi đó tập S được chia thành các nhóm là:
Nhóm 1:
Nhóm 2:
Nhóm 3:
Nhóm 4:
Nhóm 5:
Nhóm 6:
Nhóm 7:
Nhóm 8: