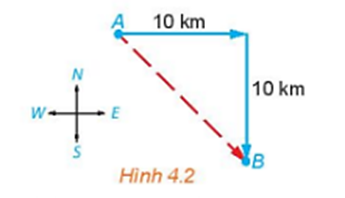
Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp 10 km
Câu hỏi:
Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp 10 km về hướng nam thì tới đảo B (H.4.2). Nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng nào và quãng đường phải dài bao nhiêu kilômét?
Trả lời:
Ta có hình vẽ sau:
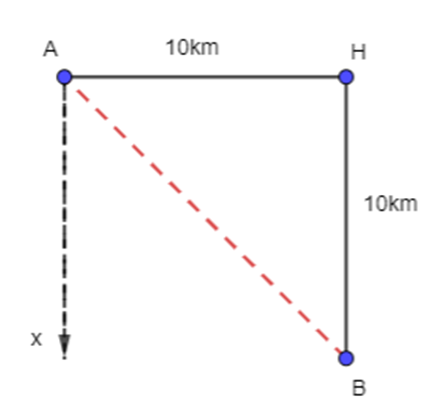
Vì góc giữa hướng đông và hướng nam là bằng 900 nên
Xét vuông ở H, ta có:
AB2 = AH2 + BH2 (định lí Py – ta – go)
AB2 = 102 + 102 = 100 + 100 = 200
vuông tại H, có AH = BH = 10 km nên cân tại H
Tia Ax là hướng nam nên
Nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng đông nam và đi quãng đường dài km.