Cho tam giác ABC với đường cao BD a) Biểu thị BD theo AB và sin A.
Câu hỏi:
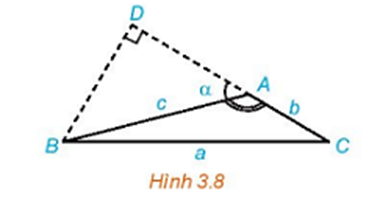
Cho tam giác ABC với đường cao BD
a) Biểu thị BD theo AB và sin A.
b) Viết công thức tính diện tích S của tam giác ABC theo b, c, sin A.
Trả lời:
a)
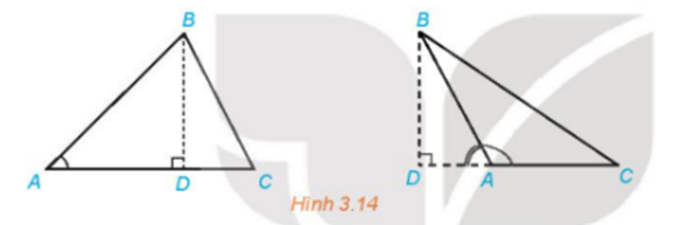
TH1: Đường cao BD nằm trong tam giác ABC
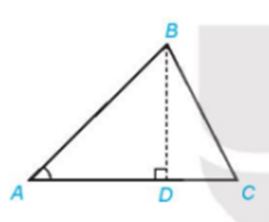
Xét ΔABD vuông tại D, có:
BD = sinA.AB
TH2: Đường cao BD nằm ngoài tam giác ABC
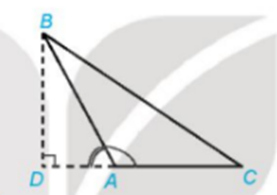
Xét ΔABD vuông tại D, có:
Vậy trong cả hai trường hợp ta đều có BD = sinA.AB.
b) TH1. Đường cao BD nằm trong tam giác ABC:
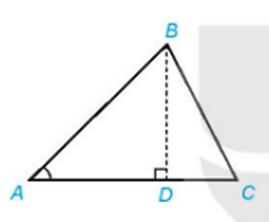
TH2. Đường cao BD nằm ngoài tam giác ABC:
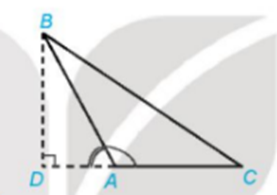
Vậy cả hai trường hợp