Ta đã biết tính cosA theo độ dài các cạnh của tam giác ABC. Liệu sinA và diện tích S
Câu hỏi:
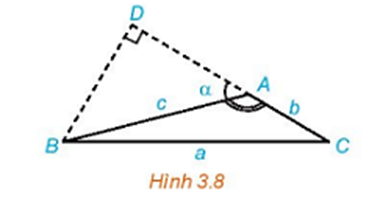
Ta đã biết tính cosA theo độ dài các cạnh của tam giác ABC. Liệu sinA và diện tích S có tính được theo độ dài cạnh của tam giác ABC không?
Trả lời:
sinA và S được tính theo độ dài cạnh của tam giác ABC như sau:
Ta có: (định lí cos)
Mà: cos2A + sin2A = 1
Û sin2A = 1 – cos2A
Þ
Do nên sin A > 0 hay
Ta có:
Khi đó diện tích tam giác ABC là:
.
Vậy sin A và diện tích S có tính được theo độ dài cạnh của tam giác ABC.