Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M
Câu hỏi:
Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.
A. \(\left| {\overrightarrow {AM} } \right| = \sqrt {53} \)cm
B. \(\left| {\overrightarrow {AM} } \right| = 3\) cm
C. \(\left| {\overrightarrow {AM} } \right| = \frac{{\sqrt {53} }}{2}\) cm
D. \(\left| {\overrightarrow {AM} } \right| = \frac{3}{2}\) cm
Trả lời:
Đáp án đúng là C
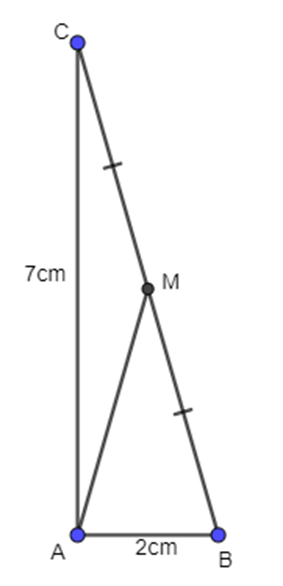
Xét tam giác ABC vuông tại A, có:
BC2 = AB2 + AC2 (định lí Py – ta – go)
⇔ BC2 = 22 + 72 = 4 + 49 = 53
⇔ BC = \(\sqrt {53} \) cm
Ta lại có M là trung điểm BC
⇒ AM = \(\frac{1}{2}\) BC (tính chất đường trung tuyến)
⇒ AM = \(\frac{{\sqrt {53} }}{2}\) cm.
⇒ \(\left| {\overrightarrow {AB} } \right| = AB = \frac{{\sqrt {53} }}{2}cm\)
Vậy độ dài vectơ \(\overrightarrow {AB} \) là \(\frac{{\sqrt {53} }}{2}cm.\)