HĐ2 trang 27 Toán 10 Tập 1 - Kết nối tri thức
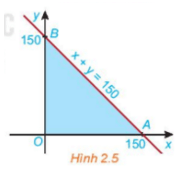
Cho đường thẳng d: x + y = 150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B.
Giải Toán lớp 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn
HĐ2 trang 27 Toán 10 Tập 1: Cho đường thẳng d: x + y = 150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B.
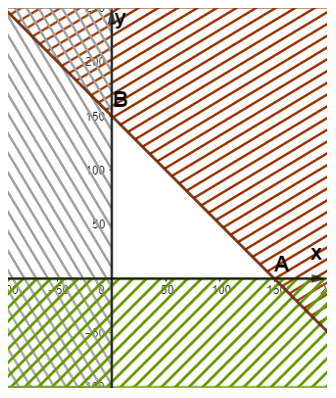
a) Xác định các miền nghiệm D1, D2, D3 của các bất phương trình tương ứng x ≥ 0, y ≥ 0 và x + y ≤ 150.
b) Miền tam giác OAB (H.2.5) có phải là giao của các miền nghiệm D1, D2, D3 hay không?
c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:
Lời giải:
a)
+ Trục Oy có phương trình x = 0 và điểm (1; 0) thỏa mãn 1 > 0, do đó miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1; 0) (tính cả bờ Oy).
+ Trục Ox có phương trình y = 0 và điểm (0; 1) thỏa mãn 1 > 0, do đó miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0; 1) (tính cả bờ Ox).
+ Xác định miền nghiệm D3 của bất phương trình x + y ≤ 150.
- Vẽ đường thẳng d: x + y – 150 = 0.
- Vì 0 + 0 = 0 < 150 nên tọa độ điểm O(0; 0) thỏa mãn bất phương trình x + y ≤ 150
Do đó miền nghiệm D3 của bất phương trình x + y ≤ 150 là nửa mặt phẳng bờ d chứa gốc tọa độ (tính cả bờ d).
b) Giao điểm của ba miền nghiệm D1, D2, D3 là miền tam giác OAB với O(0;0), A(150;0) và B(0;150)
Do đó miền tam giác OAB (H.2.5) có là giao của các miền nghiệm D1, D2, D3.
c) Điểm (1;2) nằm trong tam giác OAB thỏa mãn x = 1 > 0, y = 2 > 0 và 1 + 2 = 3 < 150 nên cặp số (x; y) = (1;2) thỏa mãn cả ba bất phương trình của hệ bất phương trình đã cho. Do đó nó là một nghiệm của hệ bất phương trình đã cho.
Điểm (1;149) nằm trên một cạnh của tam giác OAB thỏa mãn x = 1 > 0, y = 149 > 0 và 1 + 149 = 150 ≤ 150 nên cặp số (x; y) = (1;149) thỏa mãn cả ba bất phương trình của hệ bất phương trình đã cho. Do đó nó là một nghiệm của hệ bất phương trình đã cho.
Lời giải bài tập Toán 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn hay, chi tiết khác: