HĐ3 trang 28 Toán 10 Tập 1 - Kết nối tri thức
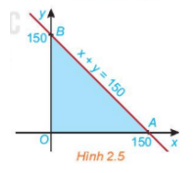
Xét biểu thức F(x; y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Tọa độ ba đỉnh là O(0;0), A(150; 0) và B(0; 150) (H.2.5).
Giải Toán lớp 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn
HĐ3 trang 28 Toán 10 Tập 1: Xét biểu thức F(x; y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Tọa độ ba đỉnh là O(0;0), A(150; 0) và B(0; 150) (H.2.5).
a) Tính giá trị của biểu thức F(x; y) tại mỗi đỉnh O, A và B.
b) Nêu nhận xét về dấu của hoành độ x và tung độ y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB.
c) Nêu nhận xét về tổng x + y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị lớn nhất của F(x; y) trên miền tam giác OAB.
Lời giải:
a) Tại O(0;0):
Thay x = 0, y = 0 vào biểu thức F(x;y) = 2x + 3y, ta được:
F(0;0) = 2.0 + 3.0 = 0.
Tại A(150;0):
Thay x = 150, y = 0 vào biểu thức F(x;y) = 2x + 3y, ta được:
F(150;0) = 2.150 + 3.0 = 300.
Tại B(0;150):
Thay x = 0, y = 150 vào biểu thức F(x;y) = 2x + 3y, ta được:
F(0;150) = 2.0 + 3.150 = 450.
b) Các điểm nằm trong miền tam giác OAB, có hoành độ x ≥ 0 và tung độ y ≥ 0.
⇒ F(x;y) = 2x + 3y ≥ 2.0 + 3.0 = 0
Do đó giá trị nhỏ nhất của F(x;y) = 0 tại O(0;0).
c) Các điểm nằm trong miền tam giác OAB có hoành độ x và tung độ y thỏa mãn: 0 ≤ x + y ≤ 150
⇔ 0 ≤ 2x + 2y ≤ 300
⇔ 0 ≤ 2x + 2y + y ≤ 300 + y
Mà 0 ≤ y ≤ 150 nên 300 + y ≤ 450
Do đó 0 ≤ 2x + 2y + y ≤ 450
⇔ 0 ≤ 2x + 3y ≤ 450 hay ⇔ 0 ≤ F(x;y) ≤ 450
Vậy giá trị lớn nhất của hàm F(x;y) = 450 tại điểm B(0;150).
Lời giải bài tập Toán 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn hay, chi tiết khác: