Luyện tập 4 trang 86 Toán 10 Tập 2 - Kết nối tri thức

Cho ba hộp A, B, C. Hộp A có chứa ba thẻ mang số 1, số 2, số 3. Hộp B chứa hai thẻ mang số 2 và số 3. Hộp C chứa hai thẻ mang số 1 và số 2. Từ mỗi hộp ta rút ra ngẫu nhiên một thẻ.

Giải Toán lớp 10 Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển

Luyện tập 4 trang 86 Toán 10 Tập 2: Cho ba hộp A, B, C. Hộp A có chứa ba thẻ mang số 1, số 2, số 3. Hộp B chứa hai thẻ mang số 2 và số 3. Hộp C chứa hai thẻ mang số 1 và số 2. Từ mỗi hộp ta rút ra ngẫu nhiên một thẻ.

a) Vẽ sơ đồ hình cây để mô tả các phần tử của không gian mẫu.

b) Gọi M là biến cố: “Trong ba thẻ rút ra có ít nhất một thẻ số 1”. Biến cố $\overline{M}$ là tập con nào của không gian mẫu?

c) Tính P(M) và P($\overline{M}$).

Lời giải:

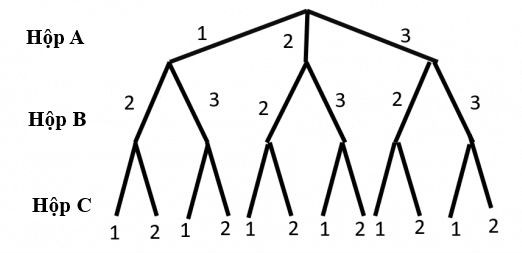
a) Theo bài ra, ta vẽ được sơ đồ hình cây mô tả các phần tử của không gian mẫu như sau:

Ta có: Ω = {121; 122; 131; 132; 221; 222; 231; 232; 321; 322; 331; 332}.

Vậy n(Ω) = 12.

b) Biến cố M: “Trong ba thẻ rút ra có ít nhất một thẻ số 1”.

Do đó, biến cố $\overline{M}$: "Trong ba thẻ rút ra không có thẻ số 1".

Khi đó: $\overline{M}$= {222; 232; 322; 332}.

c) Ta có: n($\overline{M}$)= 4.

Do đó, $P\left(\overline{M}\right)=\frac{n\left(\overline{M}\right)}{n\left(\Omega \right)}=\frac{4}{12}=\frac{1}{3}$. 

Vì $\overline{M}$ là biến cố đối của biến cố M nên $P\left(\overline{M}\right)=1-P\left(M\right)$.

Hay $P\left(M\right)=1-P\left(\overline{M}\right)=1-\frac{1}{3}=\frac{2}{3}.$

Vậy $P\left(M\right)=\frac{2}{3}$ và $P\left(\overline{M}\right)=\frac{1}{3}$.

Lời giải bài tập Toán 10 Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển hay, chi tiết khác:

• Mở đầu trang 83 Toán 10 Tập 2: Trở lại tình huống mở đầu trong Bài 26. Hãy tính xác suất trúng giải độc đắc ....

• HĐ1 trang 83 Toán 10 Tập 2: Theo định nghĩa cổ điển của xác suất để tính xác suất của biến cố F: “Bạn An trúng giải độc đắc” ....

• Luyện tập 1 trang 84 Toán 10 Tập 2: Một tổ trong lớp 10B có 12 học sinh, trong đó có 7 học sinh nam và 5 học sinh nữ ....

• HĐ2 trang 84 Toán 10 Tập 2: Trong trò chơi "Vòng quay may mắn", người chơi sẽ quay hai bánh xe ....

• Luyện tập 2 trang 85 Toán 10 Tập 2: Trở lại trò chơi “Vòng quay may mắn” ở HĐ2. Tính xác suất để người chơi nhận được loại xe 110 cc có màu trắng hoặc màu xanh ....

• Luyện tập 3 trang 85 Toán 10 Tập 2: Trong một cuộc tổng điều tra dân số, điều tra viên chọn ngẫu nhiên một gia đình có ba người con và quan tâm giới tính của ba người con này ....

• HĐ3 trang 85 Toán 10 Tập 2: Cho E là biến cố và Ω là không gian mẫu. Tính n($\overline{E}$) theo n(Ω) và n(E) ....

• Vận dụng trang 86 Toán 10 Tập 2: Giải bài toán trong tình huống mở đầu ....

• Bài 9.6 trang 86 Toán 10 Tập 2: Chọn ngẫu nhiên một gia đình có ba con và quan sát giới tính của ba người con này. Tính xác suất của các biến cố sau ....

• Bài 9.7 trang 86 Toán 10 Tập 2: Một hộp đựng các tấm thẻ đánh số 10; 11; ....; 20. Rút ngẫu nhiên từ hộp hai tấm thẻ ....

• Bài 9.8 trang 86 Toán 10 Tập 2: Một chiếc hộp đựng 6 viên bi trắng, 4 viên bi đỏ và 2 viên bi đen. Chọn ngẫu nhiên ra 6 viên bi ....

• Bài 9.9 trang 86 Toán 10 Tập 2: Gieo liên tiếp một con xúc xắc cân đối và một đồng xu cân đối ....

• Bài 9.10 trang 87 Toán 10 Tập 2: Trên một phố có hai quán ăn X, Y. Ba bạn Sơn, Hải, Văn mỗi người chọn ngẫu nhiên một quán ăn ....

• Bài 9.11 trang 87 Toán 10 Tập 2: Gieo lần lượt hai con xúc xắc cân đối. Tính xác suất để ít nhất một con xúc xắc xuất hiện mặt 6 chấm ....

• Bài 9.12 trang 87 Toán 10 Tập 2: Màu hạt của đậu Hà Lan có hai kiểu hình là màu vàng và màu xanh tương ứng với hai loại gene là gene trội A và gene lặn a ....