Một lớp học có 16 học sinh học giỏi môn Toán; 12 học sinh học giỏi môn Văn

Một lớp học có 16 học sinh học giỏi môn Toán; 12 học sinh học giỏi môn Văn; 8 học sinh vừa học giỏi môn Toán và Văn; 19 học sinh không học giỏi cả hai môn Toán và Văn. Hỏi lớp học có bao nhiêu học sinh?

A. 31;

B. 54;

C. 39;

D. 47.

Đáp án đúng là: C

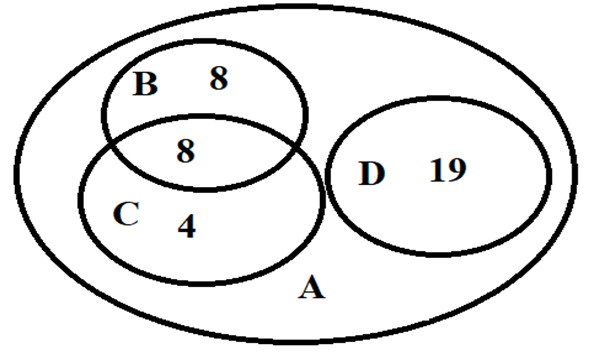
Gọi A là tập hợp gồm các học sinh trong lớp; B là tập số học sinh giỏi Toán; C là tập số học sinh giỏi Văn; D là tập số học sinh không giỏi cả 2 môn Toán và Văn.

Khi đó n(B) = 16, n(C) = 12, n(B∩C) = 8, n(D) = 19.

Số học sinh trong lớp giỏi ít nhất một trong hai môn Toán hoặc Văn là:

n(B∪C) = n(B) + n(C) - n(B∩C) = 16 + 12 – 8 = 20.

Ta có A = \((B \cup C) \cup D\)

Số học sinh trong lớp là: n(A) = n(B∪C) + n(D) = 20 + 19 = 39 (học sinh).

Được thể hiện trong biểu đồ Ven như sau: