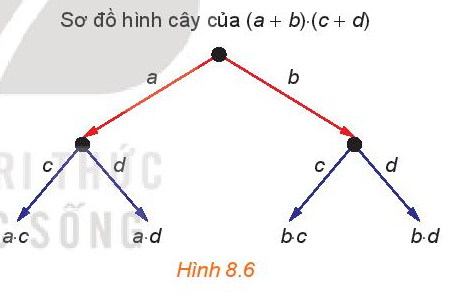
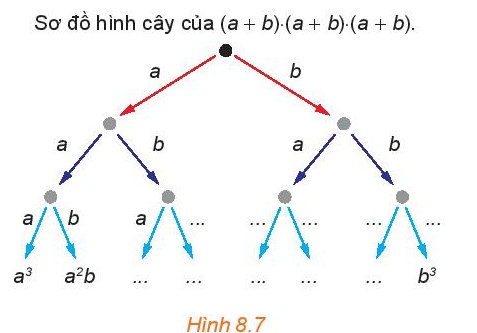
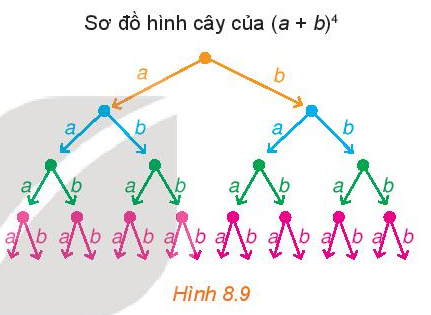
Ở lớp 8, khi học về hằng đẳng thức, ta đã biết khai triển: (a + b)2 = a2 + 2ab + b2; (a + b)3 = a3 + 3a2b + 3ab2 + b3. Quan sát các đơn thức ở vế phải của các đẳng thức trên
Câu hỏi:
A. Các câu hỏi trong bài
Ở lớp 8, khi học về hằng đẳng thức, ta đã biết khai triển:
(a + b)2 = a2 + 2ab + b2;
(a + b)3 = a3 + 3a2b + 3ab2 + b3.
Quan sát các đơn thức ở vế phải của các đẳng thức trên, hãy nhận xét về quy luật số mũ của a và b. Có thể tìm được cách tính các hệ số của đơn thức trong khai triển (a + b)n khi n ∈ {4; 5} không?
Trả lời:
Hướng dẫn giải
+) Ta có: a2 + 2ab + b2 = a2 . b0 + 2 . a1 . b1 + b2 . a0
a3 + 3a2b + 3ab2 + b3 = a3 . b0 + 3 . a2 . b1 + 3 . a1 . b2 + a0 . b3
Quan sát vế phải của các đẳng thức, ta thấy số mũ của a giảm dần từ số mũ của biểu thức vế trái đến 0, còn số mũ của b tăng dần từ 0 đến số mũ của biểu thức ở vế trái.
+) Sau khi học bài Nhị thức Newton này, ta có thể tìm được cách tính các hệ số của đơn thức trong khai triển (a + b)n khi n ∈ {4; 5}.