Khai triển (x – 2)^4.
Câu hỏi:
Khai triển (x – 2)4.
Trả lời:
Hướng dẫn giải
Thay a = x và b = – 2 trong công thức khai triển của (a + b)4, ta được:
(x – 2)4 = x4 + 4x3 . (– 2) + 6x2 . (–2)2 + 4x . (– 2)3 + (– 2)4
= x4 – 8x3 + 24x2 – 32x + 16.
Câu hỏi:
Khai triển (x – 2)4.
Trả lời:
Hướng dẫn giải
Thay a = x và b = – 2 trong công thức khai triển của (a + b)4, ta được:
(x – 2)4 = x4 + 4x3 . (– 2) + 6x2 . (–2)2 + 4x . (– 2)3 + (– 2)4
= x4 – 8x3 + 24x2 – 32x + 16.
Câu 1:
A. Các câu hỏi trong bài
Ở lớp 8, khi học về hằng đẳng thức, ta đã biết khai triển:
(a + b)2 = a2 + 2ab + b2;
(a + b)3 = a3 + 3a2b + 3ab2 + b3.
Quan sát các đơn thức ở vế phải của các đẳng thức trên, hãy nhận xét về quy luật số mũ của a và b. Có thể tìm được cách tính các hệ số của đơn thức trong khai triển (a + b)n khi n ∈ {4; 5} không?
Câu 2:
Sơ đồ hình cây của tích hai nhị thức (a + b) . (c + d) được xây dựng như sau:
• Từ một điểm gốc, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức (gọi là nhãn của mũi tên) của nhị thức thứ nhất (H.8.6);
• Từ ngọn của mỗi mũi tên đã xây dựng, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức của nhị thức thứ hai;
• Tại ngọn của các mũi tên xây dựng tại bước sau cùng, ghi lại tích của các nhãn của các mũi tên đi từ điểm gốc đến đầu mút đó.
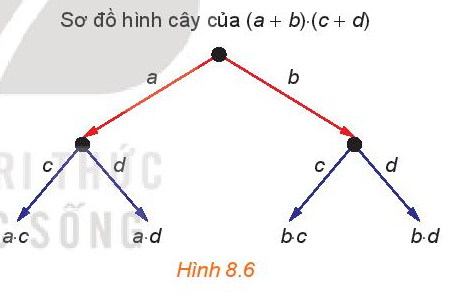
Hãy lấy tổng của các tích nhận được và so sánh kết quả với khai triển của tích (a + b) . (c + d).
Câu 3:
Hãy cho biết các đơn thức còn thiếu (...) trong sơ đồ hình cây (H.8.7) của tích (a + b) . (a + b) . (a + b).
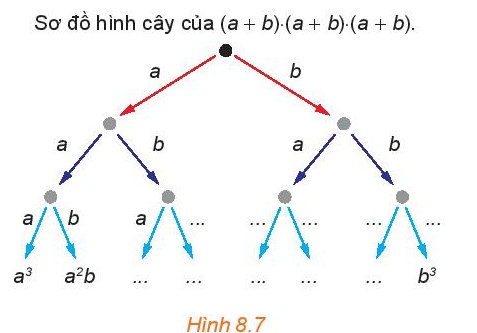
Có bao nhiêu tích nhận được lần lượt bằng a3, a2b, ab2, b3?
Hãy so sánh chúng với các hệ số nhận được khi khai triển (a + b)3.
Câu 4:
Sơ đồ hình cây của khai triển (a + b)4 được mô tả như Hình 8.9. Sau khi khai triển, ta thu được một tổng gồm 24 (theo quy tắc nhân) đơn thức có dạng x . y . z . t, trong đó mỗi x, y, z, t là a hoặc b. Chẳng hạn, nếu x, y, t là a, còn z là b thì ta có đơn thức a . a . b . a, thu gọn là a3b. Để có đơn thức này, thì trong 4 nhân tử x, y, z, t có 1 nhân tử là b, 3 nhân tử còn lại là a. Khi đó số đơn thức đồng dạng với a3b trong tổng là \(C_4^1\).
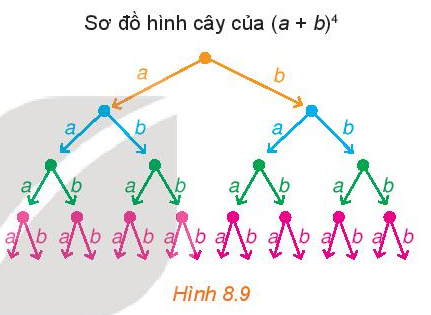
Lập luận tương tự trên, dùng kiến thức về tổ hợp, hãy cho biết trong tổng nêu trên, có bao nhiêu đơn thức đồng dạng với mỗi đơn thức thu gọn sau:
• a4; • a3b; • a2b2; • ab3; • b4.
Câu 5:
Tương tự như HĐ3, sau khi khai triển (a + b)5, ta thu được một tổng gồm 25 đơn thức có dạng x . y . z . t . u, trong đó mỗi kí hiệu x, y, z, t, u là a hoặc b. Chẳng hạn, nếu x, z là a, còn y, t, u là b thì ta có đơn thức a . b . a . b . b, thu gọn là a2b3. Để có đơn thức này, thì trong 5 nhân tử x, y, z, t, u có 3 nhân tử là b, 2 nhân tử còn lại là a. Khi đó số đơn thức đồng dạng với a2b3 trong tổng là \(C_5^3\).
Lập luận tương tự như trên, dùng kiến thức về tổ hợp, hãy cho biết, trong tổng nhận được nêu trên có bao nhiêu đơn thức đồng dạng với mỗi đơn thức thu gọn sau:
• a5; • a4b; • a3b2; • a2b3; •ab4; •b5.
Câu 7:
a) Dùng hai số hạng đầu tiên trong khai triển của (1 + 0,05)4 để tính giá trị gần đúng của 1,054.
b) Dùng máy tính cầm tay tính giá trị của 1,054 và tính sai số tuyệt đối của giá trị gần đúng nhận được ở câu a.
Câu 8:
B. Bài tập
Khai triển các đa thức:
a) (x – 3)4;
b) (3x – 2y)4;
c) (x + 5)4 + (x – 5)4;
d) (x – 2y)5.
