Tam giác ABC có các góc A = 75 độ, góc B = 45 độ. Tính tỉ số AB/AC
Câu hỏi:
Tam giác ABC có các góc \(\widehat A = 75^\circ ,\widehat B = 45^\circ \). Tính tỉ số \(\frac{{AB}}{{AC}}\).
A. \(\frac{{\sqrt 6 }}{3}\);
C. \(\frac{{\sqrt 6 }}{2}\);
Trả lời:
Đáp án đúng là: C
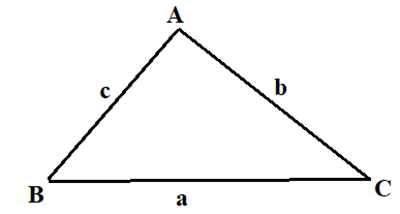
Ta có: \[\frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{AB}}{{AC}} = \frac{c}{b} = \frac{{\sin C}}{{\sin B}} = \frac{{\sin (180^\circ - 75^\circ - 45^\circ )}}{{\sin 45^\circ }} = \frac{{\sqrt 6 }}{2}\].
Xem thêm bài tập trắc nghiệm Toán 10 KNTT có lời giải hay khác:
Câu 1:
Tam giác ABC có A = 120° khẳng định nào sau đây đúng?
Xem lời giải »
Câu 3:
Hình bình hành có hai cạnh là 3 và 5, một đường chéo bằng 5. Tìm độ dài đường chéo còn lại.
Xem lời giải »
Câu 5:
Biết tanα = 2, giá trị của biểu thức \(M = \frac{{3\sin \alpha - 2\cos \alpha }}{{5\cos \alpha + 7\sin \alpha }}\) bằng:
Xem lời giải »
Câu 6:
Tam giác ABC có các góc \(\widehat B = 30^\circ ,\widehat C = 45^\circ \), AB = 3. Tính cạnh AC.
Xem lời giải »
Câu 8:
Tính diện tích tam giác ABC biết A = 60°; b = 10; c = 20.
Xem lời giải »

