Giải Toán 10 trang 23 Tập 1 Kết nối tri thức
Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 23 Tập 1 trong Bài 3: Bất phương trình bậc nhất hai ẩn Toán lớp 10 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 23.
Giải Toán 10 trang 23 Tập 1 Kết nối tri thức
HĐ2 trang 23 Toán 10 Tập 1: Cặp số (x; y) = (100; 100) thỏa mãn bất phương trình bậc nhất hai ẩn nào trong hai bất phương trình thu được ở HĐ1? Từ đó cho biết rạp chiếu phim có phải bù lỗ hay không nếu bán được 100 vé loại 1 và 100 vé loại 2.
Trả lời câu hỏi tương tự với cặp số (x; y) = (150; 150).
Lời giải:
+) Xét cặp số (x; y) = (100; 100).
- Thay x = 100 và y = 100 vào bất phương trình 50x + 100y ≥ 20 000 ta được: 50.100 + 100.100 ≥ 20 000 ⇔ 15 000 ≥ 20 000 (vô lí).
Do đó cặp số (100; 100) không thỏa mãn bất phương trình 50x + 100y ≥ 20 000.
- Thay x = 100 và y = 100 vào bất phương trình 50x + 100y < 20 000 ta được: 50.100 + 100.100 < 20 000 ⇔ 15 000 < 20 000 (luôn đúng).
Do đó cặp số (100; 100) thỏa mãn bất phương trình 50x + 100y < 20 000.
Vì vậy nếu rạp chiếu phim bán được 100 vé loại 1 và 100 vé loại 2 thì số tiền thu được là 15 triệu đồng và rạp chiếu phim phải bù lỗ.
+) Xét cặp số (x; y) = (150; 150).
- Thay x = 150 và y = 150 vào bất phương trình 50x + 100y ≥ 20 000 ta được: 50.150 + 100.150 ≥ 20 000 ⇔ 22 500 ≥ 20 000 (luôn đúng).
Do đó cặp số (150; 150) thỏa mãn bất phương trình 50x + 100y ≥ 20 000.
- Thay x = 150 và y = 150 vào bất phương trình 50x + 100y ≥ 20 000 ta được 50.150 + 100.150 < 20 000 ⇔ 22 500 < 20 000 (vô lí).
Do đó cặp số (150; 150) không thỏa mãn bất phương trình 50x + 100y < 20 000.
Vì vậy nếu rạp chiếu phim bán được 150 vé loại 1 và 150 vé loại 2 thì số tiền thu được là 22,5 triệu đồng và rạp chiếu phim không phải bù lỗ.
Luyện tập 1 trang 23 Toán 10 Tập 1: Cho bất phương trình bậc nhất hai ẩn x + 2y ≥ 0.
a) Hãy chỉ ra ít nhất hai nghiệm của bất phương trình trên.
b) Với y = 0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?
Lời giải:
a) Với x = 1, y = 2, thay vào bất phương trình ta có: 1 + 2.2 = 5 ≥ 0 (luôn đúng)
Suy ra (1;2) là nghiệm của bất phương trình đã cho.
Với x = -2, y = 1, thay vào bất phương trình ta có: -2 + 2.1 = 0 ≥ 0 (luôn đúng)
Suy ra (-2;1) là nghiệm của bất phương trình đã cho.
Với x = 7, y = -2, thay vào bất phương trình ta có: 7 + 2.(-2) = 3 ≥ 0 (luôn đúng)
Suy ra (7;-2) là nghiệm của bất phương trình đã cho.
b) Thay y = 0 vào bất phương trình đã cho ta được: x + 2.0 ≥ 0 ⇔ x ≥ 0.
Vậy với y = 0 thì có vô số giá trị của x mà x ≥ 0 thỏa mãn bất phương trình đã cho.
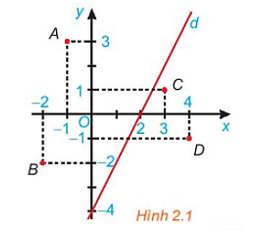
HĐ3 trang 23 Toán 10 Tập 1: Cho đường thẳng d: 2x – y = 4 trên mặt phẳng tọa độ Oxy (H.2.1). Đường thẳng này chia mặt phẳng thành hai nửa mặt phẳng.
a) Các điểm O(0; 0), A(-1; 3) và B(-2; -2) có thuộc cùng một nửa mặt phẳng bờ là đường thẳng d không?
Tính giá trị của biểu thức 2x – y tại các điểm đó và so sánh với 4.
b) Trả lời câu hỏi tương tự như câu a với các điểm C(3; 1), D(4; - 1).
Lời giải:
a) Dựa vào hình 2.1 ta thấy các điểm A, O và B thuộc cùng một nửa mặt phẳng bờ là đường thẳng d.
Thay x = 0, y = 0 vào biểu thức 2x – y ta được: 2.0 – 0 = 0 < 4.
Suy ra giá trị biểu thức 2x – y tại điểm O(0; 0) bằng 0 và nhỏ hơn 4.
Thay x = -1, y = 3 vào biểu thức 2x – y ta được: 2.(-1) – 3 = - 5 < 4.
Suy ra giá trị biểu thức 2x – y tại điểm A(-1; 3) bằng -5 và nhỏ hơn 4.
Thay x = -2, y = -2 vào biểu thức 2x – y ta được: 2.(-2) – (-2) = -2 < 4.
Suy ra giá trị biểu thức 2x – y tại điểm B(-2; 2) bằng -2 và nhỏ hơn 4.
b) Các điểm C(3; 1), D(4; - 1) cùng thuộc một nửa mặt phẳng bờ là đường thẳng d.
Thay x = 3, y = 1 vào biểu thức 2x – y ta được: 2.3 – 1 = 5 > 4.
Suy ra giá trị biểu thức 2x – y tại điểm C(3; 1) bằng 5 và lớn hơn 4.
Thay x = 4, y = -1 vào biểu thức 2x – y ta được: 2.4 – (-1) = 9 > 4.
Suy ra giá trị biểu thức 2x – y tại điểm A(4; -1) bằng 9 và lớn hơn 4.
Lời giải bài tập Toán lớp 10 Bài 3: Bất phương trình bậc nhất hai ẩn Kết nối tri thức hay khác: