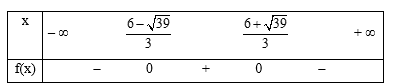Giải Toán 10 trang 24 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 24 Tập 2 trong Bài 17: Dấu của tam thức bậc hai Toán lớp 10 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 24.

Giải Toán 10 trang 24 Tập 2 Kết nối tri thức

Bài 6.15 trang 24 Toán 10 Tập 2: Xét dấu các tam thức bậc hai sau:

a) 3x² – 4x + 1; 

b) x² + 2x + 1; 

c) – x² + 3x – 2; 

d) – x² + x – 1. 

Lời giải:

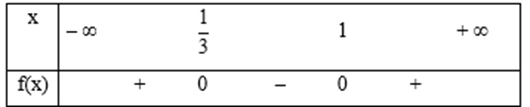
a) f(x) = 3x² – 4x + 1 có ∆' = (– 2)² – 3 . 1 = 1 > 0, hệ số a = 3 > 0 và có hai nghiệm phân biệt x₁ = $\frac{1}{3}$; x₂ = 1.

Do đó ta có bảng xét dấu f(x): 

Suy ra f(x) > 0 với mọi $x\in \left(-\infty ;\frac{1}{3}\right)\cup \left(1;+\infty \right)$ và f(x) < 0 với mọi $x\in \left(\frac{1}{3};1\right)$. 

b) f(x) = x² + 2x + 1 có ∆' = 1² – 1 . 1 = 0 và a = 1 nên f(x) có nghiệm kép x = – 1 và f(x) > 0 với mọi x ≠ – 1. 

c) f(x) = – x² + 3x – 2 có ∆ = 3² – 4 . (– 1) . (– 2) = 1 > 0, hệ số a = – 1 < 0 và có hai nghiệm phân biệt x₁ = 1; x₂ = 2.

Do đó ta có bảng xét dấu f(x): 

Suy ra f(x) > 0 với mọi x ∈ (1; 2) và f(x) < 0 với mọi x ∈ (– ∞; 1) ∪ (2; + ∞). 

d) f(x) = – x² + x – 1 có ∆ = 1² – 4 . (– 1) . (– 1) = – 3 < 0 và hệ số a = – 1 < 0 nên f(x) < 0 với mọi $x\in ℝ$. 

Bài 6.16 trang 24 Toán 10 Tập 2: Giải các bất phương trình bậc hai: 

a) x² – 1 ≥ 0; 

b) x² – 2x – 1 < 0; 

c) – 3x² + 12x + 1 ≤ 0; 

d) 5x² + x + 1 ≥ 0. 

Lời giải:

a) Tam thức f(x) = x² – 1 có ∆ = 0² – 4 . 1 . (– 1) = 4 > 0 nên f(x) có hai nghiệm x₁ = – 1 và x₂ = 1. 

Mặt khác hệ số a = 1 > 0, do đó ta có bảng xét dấu sau: 

Tập nghiệm của bất phương trình là S = (– ∞; – 1] ∪ [1; + ∞). 

b) Tam thức f(x) = x² – 2x – 1 có ∆' = (– 1)² – 1 . (– 1) = 2 > 0 nên f(x) có hai nghiệm x₁ = 1$-\sqrt{2}$ và x₂ = 1 + $\sqrt{2}$. 

Mặt khác hệ số a = 1 > 0, do đó ta có bảng xét dấu sau: 

Vậy tập nghiệm của bất phương trình là S = .

c) Tam thức f(x) = – 3x² + 12x + 1 có ∆' = 6² – (– 3) . 1 = 39 > 0 nên f(x) có hai nghiệm $x_1=\frac{6-\sqrt{39}}{3}$ và $x_2=\frac{6+\sqrt{39}}{3}$. 

Mặt khác hệ số a = – 3 < 0, do đó ta có bảng xét dấu sau: 

Vậy tập nghiệm của bất phương trình là S = $\left(-\infty ;\frac{6-\sqrt{39}}{3}\right]\cup \left[\frac{6+\sqrt{39}}{3};+\infty \right)$.

d) Tam thức f(x) = 5x² + x + 1 có ∆ = 1² – 4 . 5 . 1 = – 19 < 0 và hệ số a = 5 > 0 nên f(x) luôn dương (cùng dấu a) với mọi $x\in ℝ$. 

Vậy tập nghiệm của bất phương trình là $ℝ$. 

Bài 6.17 trang 24 Toán 10 Tập 2: Tìm các giá trị của tham số m để tam thức bậc hai sau dương với mọi $x\in ℝ$:

x² + (m + 1)x + 2m + 3. 

Lời giải:

Ta có tam thức f(x) = x² + (m + 1)x + 2m + 3 có ∆ = (m + 1)² – 4 . 1 . (2m + 3) = m² + 2m + 1 – 8m – 12 = m² – 6m – 11. 

Lại có hệ số a = 1 > 0. 

Để f(x) luôn dương (cùng dấu hệ số a) với mọi $x\in ℝ$ thì ∆ < 0. 

⇔ m² – 6m – 11 < 0. 

Xét tam thức h(m) = m² – 6m – 11 có ∆'_m = (– 3)² – 1 . (– 11) = 20 > 0 nên h(m) có hai nghiệm m₁ = $3-\sqrt{20}=3-2\sqrt{5}$ và m₂ = $3+\sqrt{20}=3+2\sqrt{5}$. 

Mặt khác ta có hệ số a_m = 1 > 0, do đó ta có bảng xét dấu sau: 

Do đó, h(m) < 0 với mọi m $\in \left(3-2\sqrt{5};3+2\sqrt{5}\right)$. 

Hay ∆ < 0 với mọi m $\in \left(3-2\sqrt{5};3+2\sqrt{5}\right)$.

Vậy m$\in \left(3-2\sqrt{5};3+2\sqrt{5}\right)$ thì tam thức bậc hai đã cho luôn dương với mọi $x\in ℝ$.

Bài 6.18 trang 24 Toán 10 Tập 2: Một vật được ném theo phương thẳng đứng xuống dưới từ độ cao 320 m với vận tốc ban đầu v₀ = 20 m/s. Hỏi sau ít nhất bao nhiêu giây, vật đó cách mặt đất không quá 100 m? Giả thiết rằng sức cản của không khí là không đáng kể?

Lời giải:

Vật được ném theo phương thẳng đứng xuống dưới từ độ cao 320 m nên vật chuyển động nhanh dần đều. 

Độ cao so với mặt đất của vật được mô tả bởi một hàm số bậc hai h(t) = v₀t + $\frac{1}{2}$gt², trong đó v₀ = 20 m/s là vận tốc ban đầu của vật, t là thời gian chuyển động tính bằng giây, g là gia tốc trọng trường (thường lấy g ≈ 10 m/s²) và độ cao h(t) tính bằng mét.  

Khi đó ta có: h(t) = 20 . t + $\frac{1}{2}$. 10 . t² hay h(t) = 5t² + 20t. 

Vật ném xuống từ độ cao 320 m nên khi vật cách mặt đất không quá 100 m có nghĩa là vật đã chuyển động được quãng đường lớn hơn hoặc bằng 320 – 100 = 220 m. 

Khi đó h(t) ≥ 220 hay 5t² + 20t ≥ 220 ⇔ t² + 4t – 44 ≥ 0 (1). 

Tam thức f(t) = t² + 4t – 44 có ∆' = 2² – 1 . (– 44) = 48 > 0 nên f(t) có hai nghiệm $t_1=-2-4\sqrt{3}$ và $t_2=-2+4\sqrt{3}$. 

Mặt khác hệ số a = 1 > 0 nên ta có bảng xét dấu: 

Suy ra bất phương trình (1) có nghiệm t ≤ $-2-4\sqrt{3}$ hoặc t ≥ $-2+4\sqrt{3}$. 

Mà thời gian t > 0 nên t ≥ $-2+4\sqrt{3}$ ≈ 4,93. 

Vậy sau ít nhất khoảng 4,93 giây thì vật đó cách mặt đất không quá 100 m. 

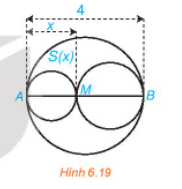
Bài 6.19 trang 24 Toán 10 Tập 2: Xét đường tròn đường kính AB = 4 và một điểm M di chuyển trên đoạn AB, đặt AM = x (H.6.19). Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của x để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ. 

Lời giải:

Vì AM = x nên x > 0, lại có AM < AB nên x < 4, vậy điều kiện của x là 0 < x < 4. 

Đường tròn lớn có đường kính AB = 4 nên bán kính của hình tròn này là R = 2. 

Diện tích hình tròn lớn này là S_R = πR² = π . 2² = 4π.  

Đường tròn nhỏ đường kính AM = x có bán kính là r₁ = $\frac{x}{2}$. 

Diện tích hình tròn nhỏ có bán kính r₁ là S₁ = πr₁² = π ${\left(\frac{x}{2}\right)}^2=\frac{x^2}{4}\pi$ . 

Ta có: AM + MB = AB ⇒ MB = AB – AM = 4 – x. 

Đường tròn đường kính MB có bán kính là r₂ = $\frac{4-x}{2}$.

Diện tích hình tròn có bán kính r₂ là S₂ = πr₂² = $\pi .{\left(\frac{4-x}{2}\right)}^2=\frac{{\left(4-x\right)}^2}{4}\pi$. 

Tổng diện tích hai hình tròn nhỏ là: 

S₁₂ = S₁ + S₂ = $\frac{x^2}{4}\pi +\frac{{\left(4-x\right)}^2}{4}\pi$ = $\frac{x^2}{4}\pi +\frac{{\left(4-x\right)}^2}{4}\pi =\frac{x^2-4x+8}{2}\pi$.

Diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ là

S(x) = S_R – S₁₂ = $4\pi -\frac{x^2-4x+8}{2}\pi =\frac{-x^2+4x}{2}\pi$. 

Vì diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ hay diện tích S(x) nhỏ hơn hoặc bằng nửa tổng diện tích hia hình tròn nhỏ hay S(x) ≤ $\frac{1}{2}{S}_{12}$. 

Khi đó:$\frac{-x^2+4x}{2}\pi \le \frac{1}{2}.\frac{x^2-4x+8}{2}\pi$

$\iff -x^2+4x\le \frac{x^2-4x+8}{2}$

⇔ – 2x² + 8x ≤ x² – 4x + 8 

⇔ 3x² – 12x + 8 ≥ 0

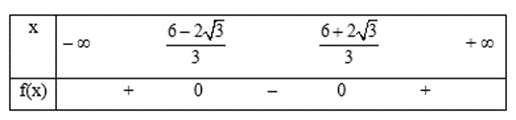
Xét tam thức f(x) = 3x² – 12x + 8 có ∆' = (– 6)² – 3 . 8 = 12 > 0 nên f(x) có hai nghiệm x₁ = $\frac{6-\sqrt{12}}{3}=\frac{6-2\sqrt{3}}{3}$ và x₂ = $\frac{6+\sqrt{12}}{3}=\frac{6+2\sqrt{3}}{3}$.

Mặt khác hệ số a = 3 > 0, do đó ta có bảng xét dấu f(x): 

Do đó f(x) ≥ 0 với mọi $x\in \left(-\infty ;\frac{6-2\sqrt{3}}{3}\right]\cup \left[\frac{6+2\sqrt{3}}{3};+\infty \right)$. 

Kết hợp với điều kiện 0 < x < 4. 

Vậy các giá trị của x thỏa mãn yêu cầu của đề bài là $x\in \left(0;\frac{6-2\sqrt{3}}{3}\right]\cup \left[\frac{6+2\sqrt{3}}{3};4\right)$. 

Lời giải bài tập Toán lớp 10 Bài 17: Dấu của tam thức bậc hai Kết nối tri thức hay khác:

• Giải Toán 10 trang 19

• Giải Toán 10 trang 20

• Giải Toán 10 trang 22

• Giải Toán 10 trang 23