Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). a) Các điểm O, A, B có thẳng
Câu hỏi:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3).
a) Các điểm O, A, B có thẳng hàng hay không?
b) Tìm điểm M(x;y) để OABM là một hình bình hành.
Trả lời:
a) Hai vecto không cùng phương (vì ). Do đó các điểm O, A, B không cùng nằm trên một đường thẳng. Vậy chúng không thẳng hàng.
b) Các điểm O, A, B không thẳng hàng
Để OABM là hình bình hành khi và chỉ khi
Ta có: nên
Vậy điểm cần tìm là M(1;2).
Xem thêm lời giải bài tập Toán 10 Kết nối tri thức hay, chi tiết:
Câu 1:
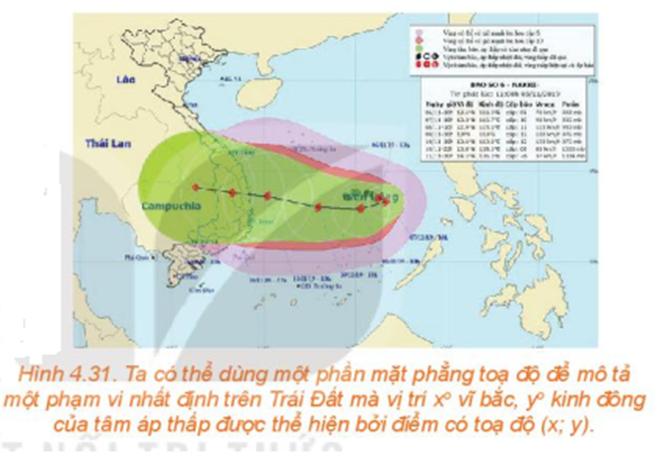
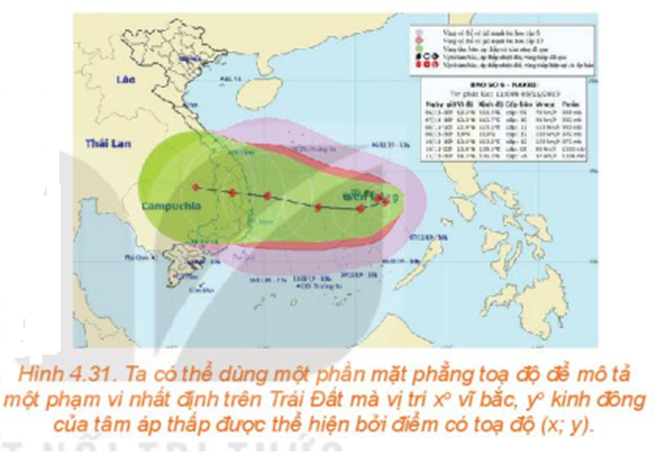
Một bản tin dự báo thời tiết thể hiện đường đi trong 12 giờ của một cơn bão trên một mặt phẳng tọa độ. ,Trong thời gian đó, tâm bão di chuyển thẳng đều từ vị trí có tọa độ (13,8; 108,3) đến vị trí tọa độ (14,1; 106,3). Dựa vào thông tin trên, liệu ta có thể dự đoán được vị trí của tâm bão tại thời điểm bất kì trong khoảng thời gian 12 giờ đó hay không?
Xem lời giải »
Câu 2:
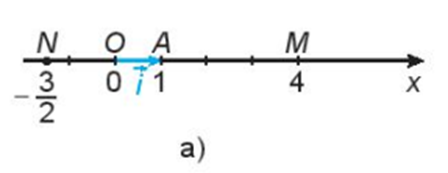
Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt (H.4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số Hãy biểu thị mỗi vectơ theo vecto đơn vị .
Xem lời giải »
Câu 3:
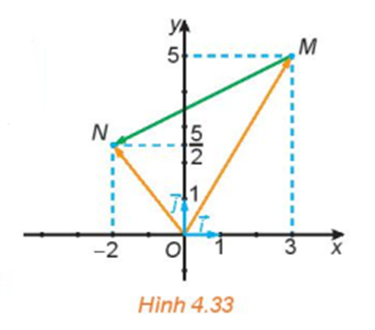
Trong Hình 4.33:
a) Hãy biểu thị mỗi vecto theo các vecto .
b) Hãy biểu thị vecto theo các vecto từ đó biểu thị vecto theo các vecto .
Xem lời giải »
Câu 5:
Từ thông tin dự báo bão được đưa ra ở đầu bài học, hãy xác định tọa độ vị trí M của tâm bão tại thời điểm 9 giờ trong khoảng thời gian 12 giờ dự báo.
Trong 12 giờ, tâm bão được dự báo di chuyển thẳng đều từ A(13,8; 108,3) tới vị trí có tọa độ B(14,1; 106,3). Gọi tọa độ của M là (x;y). Bạn hãy tìm mối liên hệ giữa hai vecto và rồi thể hiện mối quan hệ đó theo tọa độ để tìm x; y.
Xem lời giải »
Câu 6:
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2).
a) Tính độ dài của các đoạn thẳng OM, ON, MN.
b) Chứng minh rằng tam giác OMN vuông cân.
Xem lời giải »
Câu 7:
Trong mặt phẳng tọa độ Oxy, cho các vecto và các điểm M(-3;6), N(3;-3).
a) Tìm mối liên hệ giữa các vecto và
b) Các điểm O, M, N có thẳng hàng hay không?
c) Tìm điểm P(x;y) để OMNP là hình bình hành.
Xem lời giải »
Câu 8:
Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;3), B(2;4), C(-3;2).
a) Chứng minh rằng ABC là ba đỉnh của một tam giác.
b) Tìm tọa độ trung điểm M của đoạn thẳng AB.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tìm điểm D(x; y) để O(0;0) là trọng tâm tam giác ABD.
Xem lời giải »