Xét vị trí tương đối giữa các cặp đường thẳng sau: a) ∆1: x + 4y – 3 = 0 và ∆2: x – 4y – 3 = 0;
Câu hỏi:
Xét vị trí tương đối giữa các cặp đường thẳng sau:
a) ∆1: x + 4y – 3 = 0 và ∆2: x – 4y – 3 = 0;
b) ∆1: x + 2y – \(\sqrt 5 \)= 0 và ∆2: 2x + 4y – \(3\sqrt 5 \) = 0.
Trả lời:
Hướng dẫn giải
a) Xét hệ \(\left\{ \begin{array}{l}x + 4y - 3 = 0\,\,\,\,\,\,\left( 1 \right)\\x - 4y - 3 = 0\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Lấy (1) cộng vế theo vế với (2) ta được: 2x – 6 = 0 ⇔ x = 3.
Thay x = 3 vào (1) ta được: 3 + 4y – 3 = 0 ⇔ 4y = 0 ⇔ y = 0.
Do đó hệ phương trình trên có nghiệm duy nhất (x; y) = (3; 0).
Vậy hai đường thẳng ∆1 và ∆2 cắt nhau tại điểm M(3; 0).
b) Đường thẳng ∆1: x + 2y –\(\sqrt 5 \)= 0 có vectơ pháp tuyến là \({\overrightarrow n _1} = \left( {1;\,\,2} \right)\).
Đường thẳng ∆2: 2x + 4y – \(3\sqrt 5 \) = 0 có vectơ pháp tuyến là \({\overrightarrow n _2} = \left( {2;\,\,4} \right)\).
Ta thấy: \({\overrightarrow n _2} = 2{\overrightarrow n _1}\) nên hai vectơ này cùng phương.
Do đó hai đường thẳng ∆1 và ∆2 song song hoặc trùng nhau.
Mặt khác, ta lại có điểm A(\(\sqrt 5 \); 0) thuộc đường thẳng ∆1 nhưng không thuộc đường thẳng ∆2 nên hai đường thẳng này không trùng nhau.
Vậy hai đường thẳng ∆1 và ∆2 song song với nhau.
Xem thêm lời giải bài tập Toán 10 Kết nối tri thức hay, chi tiết:
Câu 1:
A. Các câu hỏi trong bài
Trong mặt phẳng tọa độ, mỗi đường thẳng đều có đối tượng đại số tương ứng, gọi là phương trình của nó. Vậy các yếu tố liên quan tới đường thẳng được thể hiện như thế nào qua phương trình tương ứng?
Xem lời giải »
Câu 2:
Trong mặt phẳng tọa độ, cho hai đường thẳng
∆1: x – 2y + 3 = 0,
∆2: 3x – y – 1 = 0.
a) Điểm M(1; 2) có thuộc cả hai đường thẳng nói trên hay không?
b) Giải hệ \(\left\{ \begin{array}{l}x - 2y + 3 = 0\\3x - y - 1 = 0\end{array} \right.\).
c) Chỉ ra mối quan hệ giữa tọa độ giao điểm của ∆1 và ∆2 với nghiệm của hệ phương trình trên.
Xem lời giải »
Câu 3:
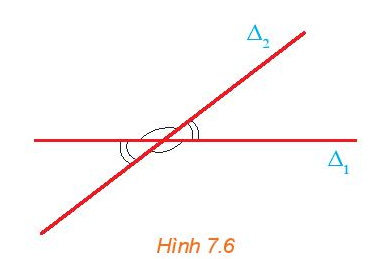
Hai đường thẳng ∆1 và ∆2 cắt nhau tạo thành bốn góc (H.7.6). Các số đo của bốn góc đó có mối quan hệ gì với nhau?
Xem lời giải »
Câu 4:
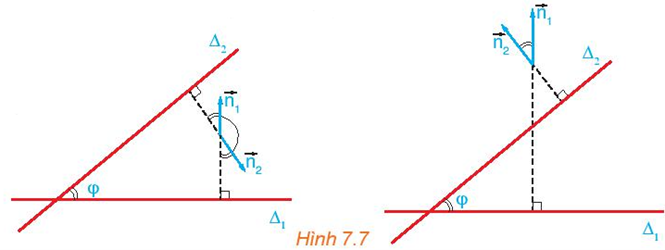
Cho hai đường thẳng cắt nhau ∆1, ∆2 tương ứng có các vectơ pháp tuyến \({\overrightarrow n _1},\,\,{\overrightarrow n _2}\). Gọi φ là góc giữa hai đường thẳng đó (H.7.7). Nêu mối quan hệ giữa:
a) góc φ và góc \(\left( {{{\overrightarrow n }_1},\,\,{{\overrightarrow n }_2}} \right)\);
b) cosφ và cos\(\left( {{{\overrightarrow n }_1},\,{{\overrightarrow n }_2}} \right)\).
Xem lời giải »
Câu 5:
Tính góc giữa hai đường thẳng
∆1: x + 3y + 2 = 0 và ∆2: y = 3x + 1.
Xem lời giải »
Câu 6:
Tính góc giữa hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 2 + t\\y = 1 - 2t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = 1 + t'\\y = 5 + 3t'\end{array} \right.\).
Xem lời giải »