Hoạt động 3 trang 97 Toán 11 Tập 1 Cánh diều
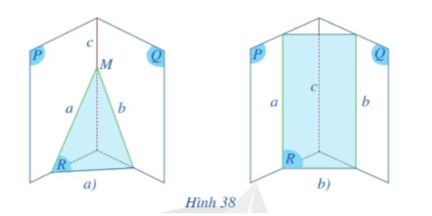
Cho ba mặt phẳng (P), (Q), (R) đôi một cắt nhau theo ba giao tuyến phân biệt a, b, c, trong đó a = (P) ∩ (R), b = (Q) ∩ (R), c = (P) ∩ (Q).
Giải Toán 11 Bài 2: Hai đường thẳng song song trong không gian - Cánh diều
Hoạt động 3 trang 97 Toán 11 Tập 1: Cho ba mặt phẳng (P), (Q), (R) đôi một cắt nhau theo ba giao tuyến phân biệt a, b, c, trong đó a = (P) ∩ (R), b = (Q) ∩ (R), c = (P) ∩ (Q).
– Nếu hai đường thẳng a và b cắt nhau tại điểm M thì đường thẳng c có đi qua điểm M hay không (Hình 38a)?
– Nếu đường thẳng a song song với đường thẳng b thì đường thẳng a có song song với đường thẳng c hay không (Hình 38b)?
Lời giải:
– Ta có: a ∩ b = {M}
Mà a ⊂ (P); b ⊂ (Q)
Nên M ∈ (P) và M ∈ (Q)
Do đó M là giao điểm của (P) và (Q).
Mà (P) ∩ (Q) = c, suy ra M ∈ c.
Vậy đường thằng c đi qua điểm M.
– Giả sử trong mặt phẳng (P) có a ∩ c = {N}.
Khi đó N ∈ a mà a ⊂ (R) nên N ∈ (R)
N ∈ c mà c ⊂ (Q) nên N ∈ (Q)
Do đó N là giao điểm của (R) và (Q).
Mà (Q) ∩ (R) = b
Suy ra N ∈ b.
Vì thế a và b có điểm chung là N (mâu thuẫn với giả thiết a và b song song).
Vậy nếu đường thẳng a song song với đường thẳng b thì đường thẳng a và b song song với đường thẳng c.
Lời giải bài tập Toán 11 Bài 2: Hai đường thẳng song song trong không gian hay, chi tiết khác: