Giải Toán 11 trang 102 Tập 1 Cánh diều
Với Giải Toán 11 trang 102 Tập 1 trong Bài 3: Đường thẳng và mặt phẳng song song Toán lớp 11 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 102.
Giải Toán 11 trang 102 Tập 1 Cánh diều
Luyện tập 1 trang 102 Toán 11 Tập 1: Quan sát các xà ngang trên sân tập thể dục Hình 47. Hãy cho biết ở vị trí tương đối của các xà ngang đó đối với mặt sàn.
Lời giải:
Vị trí tương đối của xà ngang với mặt sàn là đường thẳng song song với mặt phẳng.
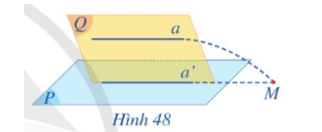
Hoạt động 2 trang 102 Toán 11 Tập 1: Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) (Hình 48). Gọi (Q) là mặt phẳng xác định bởi hai đường thẳng song song a, a’.
a) Giả sử a cắt (P) tại M. Đường thẳng a có cắt đường thẳng a’ tại M hay không?
b) Nêu vị trí tương đối của đường thẳng a và mặt phẳng (P). Vì sao?
Lời giải:
a) Do a’ ⊂ (P) và a’ ⊂ (Q) nên (P) ∩ (Q) = a’.
Mà a cắt (P) tại M nên M ∈ (P)
Lại có M ∈ a, a ⊂ (Q) nên M ∈ (Q)
Suy ra M là giao điểm của (P) và (Q).
Do đó giao tuyến a’ của hai mặt phẳng đi qua điểm M.
Vậy đường thẳng a cắt đường thẳng a’ tại M.
b) Theo câu a, nếu a cắt (P) tại M thì đường thẳng a và đường thẳng a’ cắt nhau tại M.
Điều này là mâu thuẫn với giả thiết là hai đường thẳng a và a’ song song.
Do đó a không có điểm chung với (P) nên a // (P).
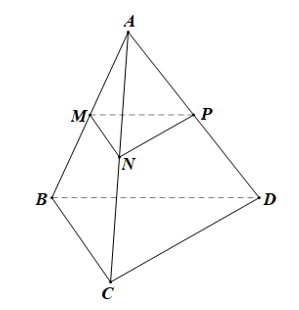
Luyện tập 2 trang 102 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD. Các đường thẳng MN, NP, PM có song song với mặt phẳng (BCD) không? Vì sao?
Lời giải:
• Xét ABC có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác
Do đó MN // BC
Lại có BC ⊂ (BCD)
Suy ra MN // (BCD).
• Chứng minh tương tự ta cũng có NP // CD.
Mà CD ⊂ (BCD)
Suy ra NP // (BCD).
• Tương tự, MP // BD mà BD ⊂ (BCD) .
Suy ra MP // (BCD).
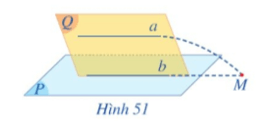
Hoạt động 3 trang 102, 103 Toán 11 Tập 1: Cho đường thẳng a song song với mặt phẳng (P). Cho mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b. (Hình 51).
a) Giả sử a cắt b tại M. Đường thẳng a có cắt mặt phẳng (P) tại M hay không?
b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao?
Lời giải:
a) Ta có a ∩ b = {M} nên M ∈ b
Mà b ⊂ (P), do đó M ∈ (P).
Lại có M ∈ a.
Vậy đường thẳng a cắt mặt phẳng (P) tại M.
b) Theo câu a, nếu a cắt b tại M thì a cắt (P) tại M, điều này mâu thuẫn với giả thiết đường thẳng a song song với mặt phẳng (P).
Do đó a và b không cắt nhau và cùng nằm trong mặt phẳng (Q).
Suy ra a // b.
Vậy hai đường thẳng a và b song song với nhau.
Lời giải bài tập Toán 11 Bài 3: Đường thẳng và mặt phẳng song song hay khác: