Giải Toán 11 trang 103 Tập 1 Cánh diều
Với Giải Toán 11 trang 103 Tập 1 trong Bài 3: Đường thẳng và mặt phẳng song song Toán lớp 11 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 103.
Giải Toán 11 trang 103 Tập 1 Cánh diều
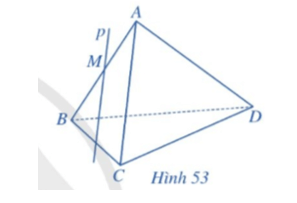
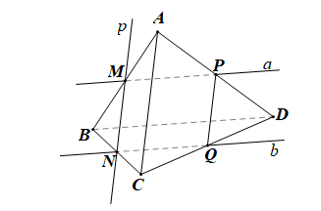
Luyện tập 3 trang 103 Toán 11 Tập 1: Ở Ví dụ 3, xác định giao tuyến của mặt phẳng (R) với các mặt phẳng (ABD), (BCD), (ACD).
Lời giải:
• Áp dụng định lí 2, ta có:
(R) đi qua M và song song với BD, mà BD ⊂ (ABD) nên mặt phẳng (R) cắt (ABD) theo giao tuyến a đi qua M và song song với BD.
• Gọi N là giao điểm của p và BC.
Khi đó N ∈ (R).
Áp dụng định lí 2, ta có:
(R) đi qua N và song song với BD, mà BD ⊂ (BCD) nên mặt phẳng (R) cắt (BCD) theo giao tuyến b đi qua N và song song với BD.
• Gọi P là giao điểm của a và AD, Q là giao điểm của b và CD.
Khi đó P ∈ (R) và P ∈ (ACD) nên P là giao điểm của (R) và (ACD);
Q ∈ (R) và Q ∈ (ACD) nên Q là giao điểm của (R) và (ACD).
Vậy (R) ∩ (ACD) = PQ.
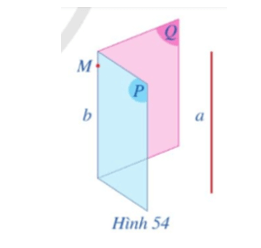
Hoạt động 4 trang 103 Toán 11 Tập 1: Cho hai mặt phẳng (P), (Q) cùng song song với đường thẳng a và (P) ∩ (Q) = b (Hình 54).
a) Lấy một điểm M trên đường thẳng b. Gọi b’, b” lần lượt là các giao tuyến của mặt phẳng (M, a) với (P) và mặt phẳng (M, a) với (Q). Cho biết b’ và b” có trùng với b hay không.
b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao?
Lời giải:
a) • Ta có: M ∈ b và (P) ∩ (Q) = b;
Suy ra M ∈ (P).
Mà M ∈ (M, a)
Do đó M là giao điểm của (P) và (M, a).
Lại có b’ = (P) ∩ (M, a)
Suy ra đường thẳng b’ đi qua M.
Tương tự ta cũng chứng minh được b’’ đi qua điểm M.
• Ta có: a // (P);
a ⊂ (M, a)
(M, a) ∩ (P) = b’
Do đó a // b’.
Tương tự ta cũng có a // b’’.
Do đó b’ // b’’.
Mặt khác: (P) ∩ (Q) = b;
(M, a) ∩ (P) = b’;
(M, a) ∩ (Q) = b’’;
b // b’’.
Do đó b // b’ // b’’.
Mà cả ba đường thẳng cùng đi qua điểm M nên ba đường thẳng này trùng nhau.
b) Vì a // b’ nên a // b (do b ≡ b’).
Lời giải bài tập Toán 11 Bài 3: Đường thẳng và mặt phẳng song song hay khác: