Thực hành 2 trang 69 Toán 11 Tập 2 Chân trời sáng tạo

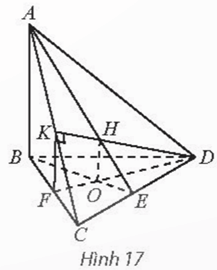
Tứ diện ABCD có AB ⊥ (BCD). Trong tam giác BCD vẽ đường cao BE và DF cắt nhau tại O. Trong mặt phẳng (ACD) vẽ DK vuông góc với AC tại K. Gọi H là trực tâm của tam giác ACD. Chứng minh rằng:

Giải Toán 11 Bài 3: Hai mặt phẳng vuông góc - Chân trời sáng tạo

Thực hành 2 trang 69 Toán 11 Tập 2: Tứ diện ABCD có AB ⊥ (BCD). Trong tam giác BCD vẽ đường cao BE và DF cắt nhau tại O. Trong mặt phẳng (ACD) vẽ DK vuông góc với AC tại K. Gọi H là trực tâm của tam giác ACD. Chứng minh rằng:

a) (ADC) ⊥ (ABE) và (ADC) ⊥ (DFK).

b) OH ⊥ (ADC).

Lời giải:

a) Ta có:

$\left.\begin{array}{l}\mathrm{AB}\perp \left(\mathrm{BCD}\right)\Rightarrow \mathrm{AB}\perp \mathrm{CD}\\ \mathrm{BE}\perp \mathrm{CE}\end{array}\right\}\Rightarrow \mathrm{CD}\perp \left(\mathrm{ABE}\right)$

Mà $\mathrm{CD}\subset \left(\mathrm{ADC}\right)$

Vậy (ADC) ⊥ (ABE)

Lại có:

$\left.\begin{array}{l}\mathrm{AB}\perp \left(\mathrm{BCD}\right)\Rightarrow \mathrm{AB}\perp \mathrm{DF}\\ \mathrm{BC}\perp \mathrm{DF}\end{array}\right\}\Rightarrow \mathrm{DF}\perp \left(\mathrm{ABC}\right)$

$\left.\begin{array}{l}\mathrm{DF}\perp \left(\mathrm{ABC}\right)\Rightarrow \mathrm{DF}\perp \mathrm{AC}\\ \mathrm{DK}\perp \mathrm{AC}\end{array}\right\}\Rightarrow \mathrm{AC}\perp \left(\mathrm{DFK}\right)$

Mà $\mathrm{AC}\subset \left(\mathrm{ADC}\right)$

Vậy (ADC) ⊥ (DFK).

b)

Ta có:

$\left.\begin{array}{l}\left(\mathrm{ADC}\right)\perp \left(\mathrm{ABE}\right)\\ \left(\mathrm{ADC}\right)\perp \left(\mathrm{DFK}\right)\\ \left(\mathrm{ABE}\right)\cap \left(\mathrm{DFK}\right)=\mathrm{OH}\end{array}\right\}\Rightarrow \mathrm{OH}\perp \left(\mathrm{ADC}\right)$

Lời giải bài tập Toán 11 Bài 3: Hai mặt phẳng vuông góc hay, chi tiết khác:

• Hoạt động khởi động trang 65 Toán 11 Tập 2: Trong thực tế, người ta thường nói mặt ngang và mặt đứng của các bậc thang vuông góc với nhau ....

• Hoạt động khám phá 1 trang 65 Toán 11 Tập 2: a) Có thể xác định góc giữa hai cánh cửa nắp hầm (Hình 1) bằng cách sử dụng góc giữa hai cây ....

• Hoạt động khám phá 2 trang 66 Toán 11 Tập 2: Từ một điểm O vẽ hai tia Ox và Oy lần lượt vuông góc với hai bức tường trong phòng ....

• Hoạt động khám phá 3 trang 67 Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d, điểm M không thuộc (P) và (Q). Gọi H và K ....

• Thực hành 1 trang 67 Toán 11 Tập 2: Cho hình chóp S.ABCD có các cạnh bên bằng nhau và đáy là hình vuông. Chứng minh rằng ....

• Vận dụng 1 trang 67 Toán 11 Tập 2: Mô tả cách kiểm tra một bức tường vuông góc với mặt sàn bằng hai cái êke trong Hình 10 ....

• Hoạt động khám phá 4 trang 67 Toán 11 Tập 2: Cho đường thẳng a vuông góc với mặt phẳng (Q). Mặt phẳng (P) chứa a và cắt (Q) theo giao tuyến c ....

• Hoạt động khám phá 5 trang 68 Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q) cùng vuông góc với mặt phẳng (R). Gọi a là giao tuyến của (P) và (Q) ....

• Vận dụng 2 trang 69 Toán 11 Tập 2: Nêu cách đặt một quyển sách lên mặt bàn sao cho tất cả các trang sách đều vuông góc với mặt bàn ....

• Hoạt động khám phá 6 trang 69 Toán 11 Tập 2: a) Cho hình lăng trụ ABCDE.A′B′C′D′E′ có cạnh bên AA′ vuông góc với một mặt phẳng đáy (Hình 18a) ....

• Thực hành 3 trang 71 Toán 11 Tập 2: Cho hình lăng trụ lục giác đều ABCDEF.A′B′C′D′E′F′ có cạnh bên bằng h và cạnh đáy bằng a ....

• Vận dụng 3 trang 71 Toán 11 Tập 2: Một chiếc lồng đèn kéo quân có dạng hình lăng trụ lục giác đều với cạnh đáy bằng 10 cm ....

• Hoạt động khám phá 7 trang 71 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông với tâm O và các cạnh bên của hình chóp bằng nhau ....

• Thực hành 4 trang 72 Toán 11 Tập 2: Cho hình chóp tứ giác đều S.ABCD có O là tâm của đáy và AB = a, SA = 2a. Tính SO theo a ....

• Vận dụng 4 trang 72 Toán 11 Tập 2: Cho biết kim tự tháp Khafre tại Ai Cập có dạng hình chóp tứ giác đều với chiều cao khoảng 136m và cạnh đáy ....

• Hoạt động khám phá 8 trang 72 Toán 11 Tập 2: Cho hình chóp đều S.A₁A₂...A₆. Mặt phẳng (P) song song với mặt đáy và cắt các cạnh bên lần lượt tại A′₁A′₂...A′₆ ....

• Thực hành 5 trang 73 Toán 11 Tập 2: Cho hình chóp cụt tam giác đều ABC.A′B′C′ có cạnh đáy lớn bằng a, cạnh đáy nhỏ ....

• Vận dụng 5 trang 73 Toán 11 Tập 2: Một người cần sơn tất cả các mặt của một cái bục để đặt tượng có dạng hình chóp cụt lục giác đều có cạnh đáy lớn 1 m ....

• Bài 1 trang 73 Toán 11 Tập 2: Cho hình chóp S.ABC có đáy là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với (ABC) ....

• Bài 2 trang 73 Toán 11 Tập 2: Cho tam giác đều ABC cạnh a, I trung điểm của BC, D là điểm đối xứng với A qua I. Vẽ đoạn thẳng SD có độ dài ....

• Bài 3 trang 73 Toán 11 Tập 2: Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy ABCD là hình thang vuông tại A và B, AA′ = 2a, AD = 2a, AB = BC = a ....

• Bài 4 trang 74 Toán 11 Tập 2: Cho hình hộp ABCD.A′B′C′D′ có đáy là hình thoi. Cho biết AB = BD = a, A′C = 2a ....

• Bài 5 trang 74 Toán 11 Tập 2: Cho hình chóp cụt tứ giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ và đường nối tâm hai đáy bằng a ....

• Bài 6 trang 74 Toán 11 Tập 2: Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m ....