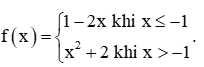Giải Toán 11 trang 75 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 75 Tập 1 trong Bài 2: Giới hạn của hàm số Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 75.

Giải Toán 11 trang 75 Tập 1 Chân trời sáng tạo

Thực hành 3 trang 75 Toán 11 Tập 1: Cho hàm số

Tìm các giới hạn $\underset{x\to -1^{+}}{\lim }f\left(x\right),\underset{x\to -1^{-}}{\lim }f\left(x\right)$ và $\underset{x\to -1}{\lim }f\left(x\right)$ (nếu có).

Lời giải:

+) Với dãy số (x_n) bất kì, x_n ≤ – 1 và x_n → – 1. Khi đó f(x_n) = 1 – 2x_n nên limf(x_n) = lim(1 – 2x_n) = 3.

Vì vậy $\underset{x\to -1^{-}}{\lim }f\left(x\right)=3$.

+) Với dãy số (x_n) bất kì, x_n > – 1 và x_n → – 1. Khi đó f(x_n) = $x_n^2+2$ nên limf(x_n) = lim($x_n^2+2$) = 3.

Vì vậy $\underset{x\to -1^{+}}{\lim }f\left(x\right)=3$.

Vì $\underset{x\to -1^{+}}{\lim }f\left(x\right)=\underset{x\to -1^{-}}{\lim }f\left(x\right)=3$ nên $\underset{x\to -1}{\lim }f\left(x\right)=3$.

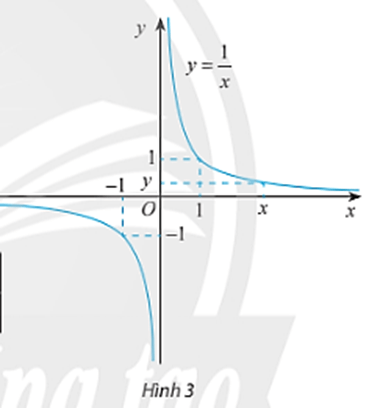
Hoạt động khám phá 4 trang 75 Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\frac{1}{x}$ có đồ thị như Hình 3.

a) Tìm các giá trị còn thiếu trong bảng sau:

x	10	100	1 000	10 000	100 000
y = f(x)	0,1	0,01	?	?	?

Từ đồ thị và bảng trên, nêu nhận xét về giá trị f(x) khi x càng lớn (dần tới +∞)?

b) Tìm các giá trị còn thiếu trong bảng sau:

x	– 100 000	– 10 000	– 1 000	– 100	– 10
y = f(x)	?	?	?	–0,01	–0,1

Từ đồ thị và bảng trên, nêu nhận xét về giá trị f(x) khi x càng bé (dần tới – ∞)?

Lời giải:

a) Với x = 1 000 suy ra $y=\frac{1}{1000}=0,001$;

Với x = 10 000 suy ra $y=\frac{1}{10000}=0,0001$;

Với x = 100 000 suy ra $y=\frac{1}{100000}=0,00001$.

Từ đó ta có bảng sau:

x	10	100	1 000	10 000	100 000
y = f(x)	0,1	0,01	0,001	0,0001	0,00001

b) Với x = – 100 000 suy ra $y=\frac{1}{-100000}=0,00001$;

Với x = – 10 000 suy ra $y=\frac{1}{-10000}=-0,0001$;

Với x = – 1 000 suy ra $y=\frac{1}{-1000}=-0,001$.

Từ đó ta có bảng sau:

x	– 100 000	– 10 000	– 1 000	– 100	– 10
y = f(x)	–0,00001	–0,0001	–0,001	–0,01	–0,1

Lời giải bài tập Toán 11 Bài 2: Giới hạn của hàm số Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 71

• Giải Toán 11 trang 72

• Giải Toán 11 trang 73

• Giải Toán 11 trang 76

• Giải Toán 11 trang 78

• Giải Toán 11 trang 79