Giải Toán 11 trang 77 Tập 2 Chân trời sáng tạo

---

Với Giải Toán 11 trang 77 Tập 2 trong Bài 4: Khoảng cách trong không gian Toán lớp 11 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 77.

Giải Toán 11 trang 77 Tập 2 Chân trời sáng tạo

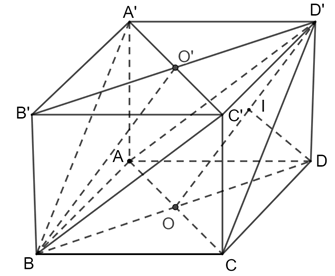
Thực hành 2 trang 77 Toán 11 Tập 2: Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính khoảng cách :

a) Giữa hai mặt phẳng (ACD′) và (A′C′B) ;

b) Giữa đường thẳng AB và (A′B′C′D′).

Lời giải:

a) Ta có $\left({\mathrm{ACD}}^{\text{'}}\right)\text{//}\left({\mathrm{BA}}^{\text{'}}{C}^{\text{'}}\right)$

$\text{⇒ d}\left(\left({\mathrm{ACD}}^{\text{'}}\right),\left({\mathrm{BA}}^{\text{'}}{C}^{\text{'}}\right)\right)=d\left(B,\left({\mathrm{ACD}}^{\text{'}}\right)\right)=d\left(D,\left({\mathrm{ACD}}^{\text{'}}\right)\right)$

Gọi I là hình chiếu vuông góc của D trên OD′.

Ta có $\left\{\begin{array}{l}\mathrm{AC}\perp \mathrm{BD}\\ \mathrm{DD}\text{'}\perp \left(\mathrm{ABCD}\right)\end{array}\right.\Rightarrow \left\{\begin{array}{l}\mathrm{AC}\perp \mathrm{BD}\\ \mathrm{DD}\text{'}\perp \mathrm{AC}\end{array}\right.$

$\Rightarrow \mathrm{AC}\perp \left({\mathrm{BDD}}^{\text{'}}{B}^{\text{'}}\right)\Rightarrow \mathrm{AC}\perp \mathrm{DI}$ và $\mathrm{DI}\perp {\mathrm{OD}}^{\text{'}}$

$\Rightarrow \mathrm{DI}\perp \left(D^{\text{'}}\mathrm{AC}\right)\Rightarrow d\left(D,\left(D^{\text{'}}\mathrm{AC}\right)\right)=\mathrm{DI}$

• Xét tam giác ABD vuông tại A nên ta có:

$\mathrm{BD}=\sqrt{{\mathrm{AB}}^2+{\mathrm{AD}}^2}=a\sqrt{2}\Rightarrow \mathrm{OD}=\frac{a\sqrt{2}}{2}.$

• Xét tam giác D′DO vuông tại D có DI là đường cao nên

$\frac{1}{{\mathrm{DI}}^2}=\frac{1}{{\mathrm{OD}}^2}+\frac{1}{D{D^{\text{'}}}^2}=\frac{2}{a^2}+\frac{1}{a^2}=\frac{3}{a^2}$

$\Rightarrow d\left(\left({\mathrm{ACD}}^{\text{'}}\right),\left(A^{\text{'}}{C}^{\text{'}}B\right)\right)=\mathrm{DI}=\frac{a\sqrt{3}}{3}.$

b) Ta có: AB // (A′B′C′D′).

Do đó d(AB, (A′B′C′D′)) = AA′ = a

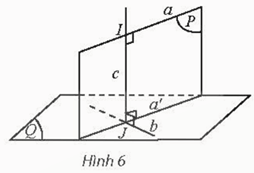
Hoạt động khám phá 3 trang 77 Toán 11 Tập 2: Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa b và song song với a. Gọi (P) là mặt phẳng chứa đường thẳng a, vuông góc với (Q) và cắt b tại J. Trong (P), gọi c là đường thẳng đi qua J vuông góc với a và cắt a tại điểm I.

Đường thẳng IJ có vuông góc với b không? Giải thích.

Lời giải:

Ta có $\left\{\begin{array}{l}\mathrm{a}\text{\hspace{0.17em}//\hspace{0.17em}}\left(\mathrm{Q}\right)\\ \mathrm{a}\text{'}=\left(\mathrm{P}\right)\cap \left(\mathrm{Q}\right)\end{array}\right.$

$\Rightarrow a\text{//}a\text{'};\mathrm{IJ}\perp a\Rightarrow \mathrm{IJ}\perp a\text{'}$

Mà (P) ⊥(Q) ⇒ IJ ⊥ (Q) $\Rightarrow$IJ ⊥ b

Lời giải bài tập Toán 11 Bài 4: Khoảng cách trong không gian hay khác:

• Giải Toán 11 trang 74

• Giải Toán 11 trang 75

• Giải Toán 11 trang 78

• Giải Toán 11 trang 81

• Giải Toán 11 trang 82