Giải Toán 11 trang 81 Tập 2 Chân trời sáng tạo

---

Với Giải Toán 11 trang 81 Tập 2 trong Bài 4: Khoảng cách trong không gian Toán lớp 11 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 81.

Giải Toán 11 trang 81 Tập 2 Chân trời sáng tạo

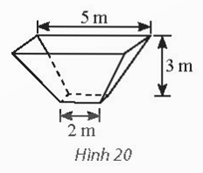
Thực hành 4 trang 81 Toán 11 Tập 2: Tính thể tích của một bồn chứa có dạng khối chóp cụt đều có kích thước được cho như trong Hình 20.

Lời giải:

Diện tích đáy lớn là: S = 5² = 25 (m²)

Diện tích đáy bé là: S′ = 2² = 4 (m²)

Thể tích của bồn chứa là: $V=\frac{1}{3}.3\left(25+\sqrt{25.4}+4\right)=39\left(m^3\right)$

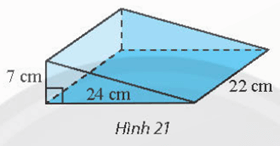
Vận dụng 3 trang 81 Toán 11 Tập 2: Tính thể tích cái nêm hình lăng trụ đứng có kích thước như trong Hình 21.

Lời giải:

Ta có khối nêm là lăng trụ đứng có đáy là tam giác vuông có các cạnh góc vuông lần lượt là 7cm và 24 cm.

Do đó diện tích đáy là: $S=\frac{1}{2}.7.24=84\left({\mathrm{cm}}^2\right)$

Chiều cao của khối lăng trụ là h = 22 cm

Thể tích của khối nêm là: V = S.h = 84.22 = 1848 (cm³)

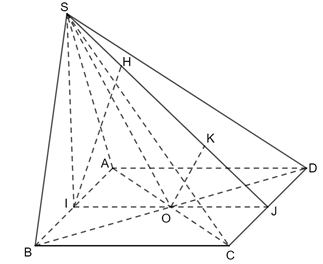
Bài 1 trang 81 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a có O là giao điểm của hai đường chéo, $\widehat{\mathrm{ABC}}=60°,\mathrm{SO}\perp \left(\mathrm{ABCD}\right),$ $\mathrm{SO}=a\sqrt{3}$ . Tính khoảng cách từ O đến mặt phẳng (SCD).

Lời giải:

Kẻ OI ⊥ CD, OH ⊥ SI

Ta có: $\left\{\begin{array}{l}\mathrm{SO}\perp \left(\mathrm{ABCD}\right)\\ \mathrm{OI}\perp \mathrm{CD}\end{array}\right.\Rightarrow \left\{\begin{array}{l}\mathrm{CD}\perp \mathrm{SO}\\ \mathrm{OI}\perp \mathrm{CD}\end{array}\right.\Rightarrow \mathrm{CD}\perp \left(\mathrm{SOI}\right)\Rightarrow \mathrm{CD}\perp \mathrm{OH}$

Mà OH ⊥ SI Suy ra OH ⊥ (SCD)

Do đó d(O, (SCD)) = OH.

Ta có: ΔABC đều $\Rightarrow$ AC = a $\Rightarrow \mathrm{OC}=\frac{1}{2}\mathrm{AC}=\frac{a}{2}$

• Xét ΔABD, áp dụng định lí cos, ta có:

$\mathrm{BD}=\sqrt{{\mathrm{AB}}^2+{\mathrm{AD}}^2-2.\mathrm{AB}.\mathrm{AD}.\cos \widehat{\mathrm{BAD}}}=a\sqrt{3}$

$\Rightarrow \mathrm{OD}=\frac{1}{2}\mathrm{BD}=\frac{a\sqrt{3}}{2}$

• Xét ΔOCD vuông tại O có OI là đường cao:

$\frac{1}{{\mathrm{OI}}^2}=\frac{1}{{\mathrm{OC}}^2}+\frac{1}{{\mathrm{OD}}^2}\Rightarrow \mathrm{OI}=\frac{a\sqrt{3}}{4}$

Ta có SO ⊥ (ABCD) $\Rightarrow$SO ⊥ OI

Do đó, tam giác SOI vuông tại O có OH là đường cao nên

$\frac{1}{{\mathrm{OH}}^2}=\frac{1}{{\mathrm{SO}}^2}+\frac{1}{{\mathrm{OI}}^2}\Rightarrow \mathrm{OH}=\frac{a\sqrt{51}}{17}$

$\Rightarrow d\left(O,\left(\mathrm{SCD}\right)\right)=\frac{a\sqrt{51}}{17}.$

Vậy khoảng cách từ O đến mặt phẳng (SCD) là $\frac{a\sqrt{51}}{17}$.

Bài 2 trang 81 Toán 11 Tập 2: Cho hai tam giác cân ABC và ABD có đáy chung AB và không cùng nằm trong một mặt phẳng.

a) Chứng minh rằng AB ⊥ CD.

b) Xác định đoạn vuông góc chung của AB và CD.

Lời giải:

a) Gọi M là trung điểm của AB.

Ta có $\left\{\begin{array}{l}\mathrm{CM}\perp \mathrm{AB}\\ \mathrm{DM}\perp \mathrm{AB}\end{array}\right.\Rightarrow \mathrm{AB}\perp \left(\mathrm{MCD}\right)\Rightarrow \mathrm{AB}\perp \mathrm{CD}$

b) Gọi H là hình chiếu vuông góc M của trên CD.

Ta có $\left\{\begin{array}{l}\left(\mathrm{CMD}\right)\perp \mathrm{AB}\\ \mathrm{C}\text{D}\perp \mathrm{MH}\end{array}\right.\Rightarrow \left\{\begin{array}{l}\mathrm{MH}\perp \mathrm{AB}\\ \mathrm{C}\text{D}\perp \mathrm{MH}\end{array}\right.$

Do đó MH là đoạn vuông góc chung của AB và CD.

Bài 3 trang 81 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, $\mathrm{SA}=\mathrm{SB}=\mathrm{SC}=\mathrm{SD}=a\sqrt{2}$ . Gọi I, J lần lượt là trung điểm của AB và CD.

a) Chứng minh AB ⊥ (SIJ).

b) Tính khoảng cách giữa hai đường thẳng AB và SC.

Lời giải:

a) Ta có: ΔSAB cân tại S và đáy là hình vuông ABCD.

$\Rightarrow \left\{\begin{array}{l}\mathrm{SI}\perp \mathrm{AB}\\ \mathrm{IJ}\perp \mathrm{AB}\end{array}\right.\Rightarrow \mathrm{AB}\perp \left(\mathrm{SIJ}\right).$

b) Ta có: AB // CD ⇒ AB // (ABCD)

$\Rightarrow$ d(AB, SC) = d(AB, (SCD)) = d(I, (SCD))

Gọi H, K lần lượt là hình chiếu vuông góc của I, O trên SJ

Ta có $\left\{\begin{array}{l}\mathrm{IH}//\mathrm{OK}\\ \mathrm{IH}=2\text{O}\mathrm{K}\end{array}\right.$

Vì AB // CD nên CD ⊥ (SIJ) $\Rightarrow$ CD ⊥ IH $\Rightarrow$IH ⊥ (SCD)

$\Rightarrow$ d(AB, CD) = d(AB, (SCD)) = IH = 2OK

Ta có: ABCD là hình vuông

$\Rightarrow$ $\mathrm{OA}=\frac{\mathrm{AC}}{2}=\frac{\sqrt{{\mathrm{AD}}^2+{\mathrm{CD}}^2}}{2}=\frac{a\sqrt{2}}{2}$

• Xét ΔSAO vuông tại O có

$\mathrm{SO}=\sqrt{{\mathrm{SA}}^2-{\mathrm{OA}}^2}=\frac{a\sqrt{6}}{2}.$

• Xét ΔSOJ vuông tại O có đường cao OK nên

$\mathrm{OK}=\frac{\mathrm{SO}.\text{OJ}}{\sqrt{{\mathrm{SO}}^2+{\mathrm{OJ}}^2}}=\frac{a\sqrt{42}}{14}$

Do đó $d\left(\mathrm{AB},\mathrm{SC}\right)=2\text{O}K=\frac{a\sqrt{42}}{7}$.

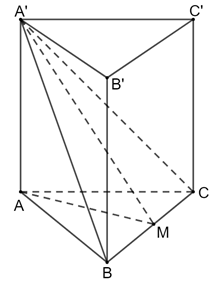
Bài 4 trang 81 Toán 11 Tập 2: Cho hình lăng trụ tam giác đều ABC.A′B′C′ có AB = a, góc giữa hai mặt phẳng (A′BC) và (ABC) bằng 60°.

a) Tính khoảng cách giữa hai đáy của hình lăng trụ.

b) Tính thể tích của khối lăng trụ.

Lời giải:

a) Vì khối lăng trụ đều nên gọi là trung điểm của BC AM ⊥ BC. Do đó góc giữa hai mặt phẳng ((A′BC), (ABC)) = $\widehat{\mathrm{SMA}}=60°$ .

Do đó khoảng cách giữa hai đáy của lăng trụ là:

${\mathrm{AA}}^{\text{'}}=\mathrm{AM}.\tan \widehat{\mathrm{SMA}}=\frac{a\sqrt{3}}{2}\tan 60°=\frac{3a}{2}.$

b) Thể tích khối lăng trụ là: $V={\mathrm{AA}}^{\text{'}}.S_{\mathrm{\Delta ABC}}=\frac{3a}{2}.\frac{a^2\sqrt{3}}{2}=\frac{3\sqrt{3}}{4}{a}^3.$

Bài 5 trang 81 Toán 11 Tập 2: Một cây cầu dành cho người đi bộ (Hình 22) có mặt sàn cầu cách mặt đường 3,5 m, khoảng cách từ đường thẳng a nằm trên tay vịn của cầu đến mặt sàn cầu là 0,8 m. Gọi b là đường thẳng kẻ theo tim đường. Tính khoảng cách giữa hai đường thẳng a và b.

Lời giải:

Vì tay vịn cầu song song với mặt đường nên khoảng cách giữa hai đường thẳng a và b

chính bằng khoảng cách từ đường thẳng a xuống mặt đường.

Khoảng cách giữa hai đường thẳng a và b bằng: 3,5 + 0,8 = 4,3(m).

Vậy khoảng cách giữa hai đường thẳng a và b là 4,3 m.

Lời giải bài tập Toán 11 Bài 4: Khoảng cách trong không gian hay khác:

• Giải Toán 11 trang 74

• Giải Toán 11 trang 75

• Giải Toán 11 trang 77

• Giải Toán 11 trang 78

• Giải Toán 11 trang 82