Bài 4.45 trang 103 Toán 11 Tập 1 - Kết nối tri thức
Cho hình hộp ABCD.ABCD. Gọi M, N lần lượt là trung điểm của cạnh AD, AB. Chứng minh rằng:
Giải Toán 11 Bài tập cuối chương 4 - Kết nối tri thức
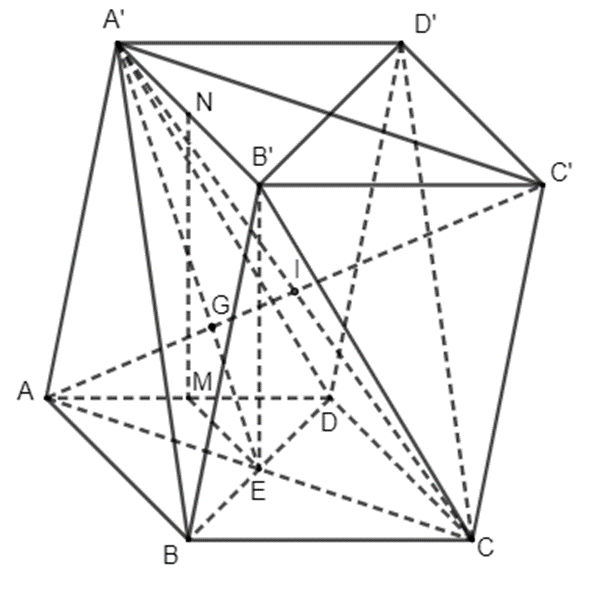
Bài 4.45 trang 103 Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Gọi M, N lần lượt là trung điểm của cạnh AD, A'B'. Chứng minh rằng:
a) BD // B'D', (A'BD) // (CB'D') và MN // (BDD'B');
b) Đường thẳng AC' đi qua trọng tâm G của tam giác A'BD.
Lời giải:
a) Vì ABCD.A'B'C'D' là hình hộp nên các mặt của nó là hình bình hành và các cạnh bên AA', BB', CC', DD' đôi một song song và bằng nhau.
Xét tứ giác BDD'B' có BB' = DD' và BB' // DD' nên BDD'B' là hình bình hành.
Suy ra BD // B'D'. Do đó, BD // (CB'D').
Vì A'B'C'D' là hình bình hành nên A'D' // B'C' và A'D' = B'C'.
Vì BCC'B' là hình bình hành nên BC // B'C' và BC = B'C'.
Do đó, A'D' // BC và A'D' = BC nên A'D'CB là hình bình hành.
Suy ra A'B // D'C. Do đó, A'B // (CB'D').
Mặt phẳng (A'BD) chứa hai đường thẳng cắt nhau BD và A'B cùng song song với mặt phẳng (CB'D') nên (A'BD) // (CB'D').
Gọi E là giao điểm hai đường chéo AC và BD của hình bình hành ABCD. Khi đó E là trung điểm của AC và BD. Lại có M là trung điểm của AD nên ME là đường trung bình của tam giác ABD, suy ra ME // AB và ME = AB (1).
Vì N là trung điểm của A'B' nên NB' = . Mà AB = A'B' và AB // A'B' nên suy ra NB' // AB và NB' = AB (2).
Từ (1) và (2) suy ra ME // NB' và ME = NB' nên tứ giác MEB'N là hình bình hành.
Suy ra MN // B'E.
Vì E thuộc BD nên E thuộc mặt phẳng (BDD'B'), do đó đường thẳng B'E nằm trong mặt phẳng (BDD'B').
Vậy MN // (BDD'B').
b) Vì E thuộc AC nên E thuộc mặt phẳng (ACC'A').
Trong mặt phẳng (ACC'A') gọi G là giao điểm của A'E và AC', gọi I là giao điểm của AC' và AC.
Mà E thuộc BD nên E thuộc mặt phẳng (A'BD) nên A'E nằm trong mặt phẳng (A'BD). Vì G thuộc A'E nên G thuộc mặt phẳng (A'BD). Do đó, G là giao điểm của AC' và mặt phẳng (A'BD).
Tứ giác ACCA' có AA' = CC' và AA' // CC' nên ACC'A' là hình bình hành.
Suy ra I là giao điểm của hai đường chéo AC' và A'C nên I là trung điểm của AC' và A'C.
Xét tam giác AA'C có AI, A'E là các đường trung tuyến và G là giao của AI và A'E (do G là giao của AC' và A'E) nên G là trọng tâm của tam giác AA'C.
Suy ra .
Xét tam giác A'BD có A'E là đường trung tuyến (do E là trung điểm của BD) và nên G là trọng tâm của tam giác A'BD.
Vậy đường thẳng AC' đi qua trọng tâm G của tam giác A'BD.
Lời giải bài tập Toán 11 Bài tập cuối chương 4 hay, chi tiết khác:
Bài 4.35 trang 102 Toán 11 Tập 1: Cho đường thẳng a song song với mặt phẳng (P) ....
Bài 4.38 trang 102 Toán 11 Tập 1: Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau ....