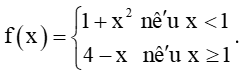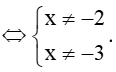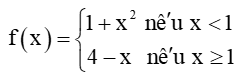Bài 5.15 trang 122 Toán 11 Tập 1 - Kết nối tri thức

Xét tính liên tục của các hàm số sau trên tập xác định của chúng:

Giải Toán 11 Bài 17: Hàm số liên tục - Kết nối tri thức

Bài 5.15 trang 122 Toán 11 Tập 1: Xét tính liên tục của các hàm số sau trên tập xác định của chúng:

a) $f\left(x\right)=\frac{x}{x^2+5x+6}$;

b)

Lời giải:

a) $f\left(x\right)=\frac{x}{x^2+5x+6}$

Biểu thức $\frac{x}{x^2+5x+6}$ có nghĩa khi x² + 5x + 6 ≠ 0 ⇔ (x + 2)(x + 3) ≠ 0

Do đó, tập xác định của hàm số f(x) là ℝ \ {– 3; – 2} = (–∞; – 3) ∪ (– 3; – 2) ∪ (– 2; +∞).

Vì f(x) là hàm phân thức hữu tỉ nên nó liên tục trên tập xác định.

Vậy hàm số f(x) liên tục trên các khoảng (–∞; – 3), (– 3; – 2) và (– 2; +∞).

b)

Tập xác định của hàm số là ℝ.

+) Nếu x < 1, thì f(x) = 1 + x².

Đây là hàm đa thức nên có tập xác định là ℝ.

Vậy nó liên tục trên (–∞; 1).

+) Nếu x > 1, thì f(x) = 4 – x.

Đây là hàm đa thức nên có tập xác định là ℝ.

Vậy nó liên tục trên (1; +∞).

+) Ta có: $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\left(4-x\right)=4-1=3$;

$\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }\left(1+x^2\right)=1+1^2=2$.

Suy ra $\underset{x\to 1^{+}}{\lim }f\left(x\right)\ne \underset{x\to 1^{-}}{\lim }f\left(x\right)$, do đó không tồn tại giới hạn của f(x) tại x = 1.

Khi đó, hàm số f(x) không liên tục tại x = 1.

Vậy hàm số đã cho liên tục trên các khoảng (–∞; 1), (1; +∞) và gián đoạn tại x = 1.

Lời giải bài tập Toán 11 Bài 17: Hàm số liên tục hay, chi tiết khác:

• Mở đầu trang 119 Toán 11 Tập 1: Một người lái xe từ địa điểm A đến địa điểm B trong thời gian 3 giờ ....

• HĐ1 trang 119 Toán 11 Tập 1: Nhận biết tính liên tục của hàm số tại một điểm ....

• Luyện tập 1 trang 120 Toán 11 Tập 1: Xét tính liên tục của hàm số ....

• HĐ2 trang 120 Toán 11 Tập 1: Cho hai hàm số ....

• Luyện tập 2 trang 121 Toán 11 Tập 1: Tìm các khoảng trên đó hàm số $f\left(x\right)=\frac{x^2+1}{x+2}$ liên tục ....

• HĐ3 trang 121 Toán 11 Tập 1: Cho hai hàm số f(x) = x² và g(x) = – x + 1. ....

• Bài 5.14 trang 122 Toán 11 Tập 1: Cho f(x) và g(x) là các hàm số liên tục tại x = 1 ....

• Bài 5.16 trang 122 Toán 11 Tập 1: Tìm giá trị của tham số m để hàm số ....

• Bài 5.17 trang 122 Toán 11 Tập 1: Một bảng giá cước taxi được cho như sau: ....