Cho hình lập phương ABCD.A'B'C'D' có cạnh a. a) Chứng minh rằng hai mặt phẳng (D'AC) và (BC'A') song song với nhau và DB' vuông góc với hai mặt phẳng đó.
Câu hỏi:
Cho hình lập phương ABCD.A'B'C'D' có cạnh a.
a) Chứng minh rằng hai mặt phẳng (D'AC) và (BC'A') song song với nhau và DB' vuông góc với hai mặt phẳng đó.
Trả lời:
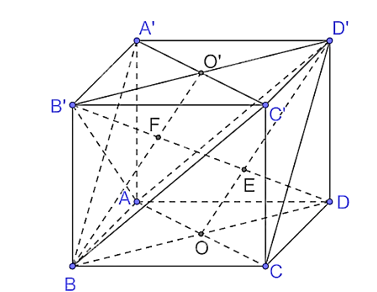
a) Vì AA' // CC' và AA' = CC' (do chúng cùng song song và bằng BB') nên AA'C'C là hình bình hành, suy ra AC // A'C' do đó A'C' // (D'AC).
Vì AB // C'D' và AB = C'D' (do chúng cùng song song và bằng CD) nên ABC'D' là hình bình hành suy ra BC' // AD', do đó BC' // (D'AC).
Vì A'C' // (D'AC) và BC' // (D'AC) nên (BC'A') // (D'AC).
Vì ABCD là hình vuông nên AC ^ BD.
Vì BB' ^ (ABCD) nên BB' ^ AC mà AC ^ BD nên AC ^ (BB'D), suy ra AC ^ DB'.
Vì AC // A'C' mà AC ^ DB' nên A'C' ^ DB'.
Do AD ^ (ABB'A') nên AD ^ A'B.
Vì ABB'A' là hình vuông nên AB' ^ A'B mà AD ^ A'B nên A'B ^ (ADB').
Suy ra A'B ^ DB'.
Có A'C' ^ DB' và A'B ^ DB' nên DB' ^ (BC'A').
Vì A'D' // BC và A'D' = BC (do chúng cùng song song và bằng AD) nên A'D'CB là hình bình hành, suy ra A'B // D'C mà A'B ^ DB' nên D'C ^ DB'.
Có AC ^ DB' và D'C ^ DB' nên DB' ^ (D'AC).