Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, và OC = 2a. Tính khoảng cách từ điểm O đến mặt phẳng ABC.
Câu hỏi:
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, và OC = 2a. Tính khoảng cách từ điểm O đến mặt phẳng ABC.
Trả lời:
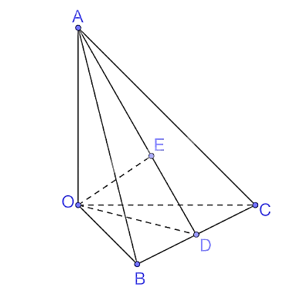
Kẻ OD ^ BC tại D.
Có OA ^ OB, OA ^ OC nên OA ^ (OBC), suy ra OA ^ BC mà OD ^ BC nên
BC ^ (OAD).
Kẻ OE ^ AD tại E.
Vì BC ^ (OAD) nên BC ^ OE mà OE ^ AD nên OE ^ (ABC).
Do đó d(O, (ABC)) = OE.
Xét tam giác OBC vuông tại O, OD là đường cao có:
.
Vì OA ^ (OBC) nên OA ^ OD.
Xét tam giác AOD vuông tại O, OE là đường cao nên
.
Vậy d(O, (ABC)) .
