Giải các phương trình sau: a) căn bậc hai của 3 tan 2x = - 1; b) tan 3x + tan 5x = 0.
Câu hỏi:
Giải các phương trình sau:
a) \(\sqrt 3 \tan 2x = - 1\);
b) tan 3x + tan 5x = 0.
Trả lời:
Lời giải:
a) \(\sqrt 3 \tan 2x = - 1\)
\( \Leftrightarrow \tan 2x = - \frac{1}{{\sqrt 3 }}\)
\( \Leftrightarrow \tan 2x = \tan \left( { - \frac{\pi }{6}} \right)\)
\( \Leftrightarrow 2x = - \frac{\pi }{6} + k\pi \,,\,k \in \mathbb{Z}\)
\( \Leftrightarrow x = - \frac{\pi }{{12}} + k\frac{\pi }{2},\,k \in \mathbb{Z}\)
Vậy phương trình đã cho có nghiệm là \(x = - \frac{\pi }{{12}} + k\frac{\pi }{2},\,k \in \mathbb{Z}\).
b) tan 3x + tan 5x = 0
⇔ tan 3x = – tan 5x
⇔ tan 3x = tan (– 5x)
⇔ 3x = – 5x + kπ, k ∈ ℤ
⇔ 8x = kπ, k ∈ ℤ
⇔ x = \(k\frac{\pi }{8},\,k \in \mathbb{Z}\)
Mà tan x có nghĩa khi x \( \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
Vậy phương trình đã cho có nghiệm là x = \(k\frac{\pi }{8}\) với \(k \ne 4 + 8n,\,\,n \in \mathbb{Z}\).
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết:
Câu 1:
Một quả đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu có độ lớn v0 không đổi. Tìm góc bắn α để quả đạn pháo bay xa nhất, bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất.
Xem lời giải »
Câu 2:
Cho hai phương trình 2x – 4 = 0 và (x – 2)(x2 + 1) = 0.
Tìm và so sánh tập nghiệm của hai phương trình trên.
Xem lời giải »
Câu 3:
Xét sự tương đương của hai phương trình sau:
\(\frac{{x - 1}}{{x + 1}} = 0\) và x2 – 1 = 0.
Xem lời giải »
Câu 4:
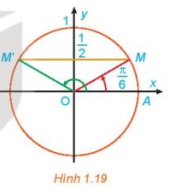
a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng [0; 2π).
b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.
Xem lời giải »
Câu 5:
a) Quan sát Hình 1.25, hãy cho biết đường thẳng y = – 1 cắt đồ thị hàm số y = cot x tại mấy điểm trên khoảng (0; π)?
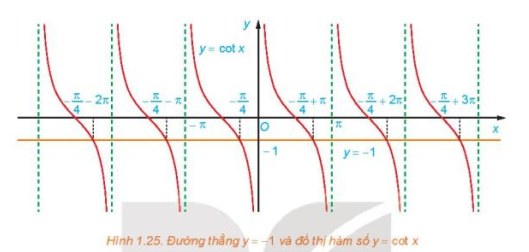
b) Dựa vào tính tuần hoàn của hàm côtang, hãy viết công thức nghiệm của phương trình đã cho.
Xem lời giải »
Câu 6:
Giải các phương trình sau:
a) cot x = 1;
b) \(\sqrt 3 \cot x + 1 = 0\).
Xem lời giải »
Câu 7:
Sử dụng máy tính cầm tay, tìm số đo độ và rađian của góc α, biết:
a) cos α = – 0,75;
b) tan α = 2,46;
c) cot α = – 6,18.
Xem lời giải »
Câu 8:
Giải các phương trình sau:
a) \(\sin x = \frac{{\sqrt 3 }}{2}\);
b) \(2\cos x = - \sqrt 2 \);
c) \(\sqrt 3 \tan \left( {\frac{x}{2} + 15^\circ } \right) = 1\);
d) \(\cot \left( {2x - 1} \right) = \cot \frac{\pi }{5}\).
Xem lời giải »


