Giải các phương trình sau: a) sin x = căn 2 /2; b) sin 3x = – sin 5x.
Câu hỏi:
Giải các phương trình sau:
a) \(\sin x = \frac{{\sqrt 2 }}{2}\);
b) sin 3x = – sin 5x.
Trả lời:
Lời giải:
a) \(\sin x = \frac{{\sqrt 2 }}{2}\)
\( \Leftrightarrow \sin x = \sin \frac{\pi }{4}\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k2\pi \\x = \pi - \frac{\pi }{4} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k2\pi \\x = \frac{{3\pi }}{4} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Vậy phương trình \(\sin x = \frac{{\sqrt 2 }}{2}\) có các nghiệm là \(x = \frac{\pi }{4} + k2\pi ,\,\,k \in \mathbb{Z}\) và \(x = \frac{{3\pi }}{4} + k2\pi \), \(k \in \mathbb{Z}\).
b) sin 3x = – sin 5x
⇔ sin 3x = sin (– 5x)
\( \Leftrightarrow \left[ \begin{array}{l}3x = - 5x + k2\pi \\3x = \pi - \left( { - 5x} \right) + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}3x = - 5x + k2\pi \\3x = \pi + 5x + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}8x = k2\pi \\ - 2x = \pi + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}x = k\frac{\pi }{4}\\x = - \frac{\pi }{2} + k\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)
Vậy phương trình đã cho có các nghiệm là \(x = k\frac{\pi }{4},\,k \in \mathbb{Z}\) và \(x = - \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết:
Câu 1:
Một quả đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu có độ lớn v0 không đổi. Tìm góc bắn α để quả đạn pháo bay xa nhất, bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất.
Xem lời giải »
Câu 2:
Cho hai phương trình 2x – 4 = 0 và (x – 2)(x2 + 1) = 0.
Tìm và so sánh tập nghiệm của hai phương trình trên.
Xem lời giải »
Câu 3:
Xét sự tương đương của hai phương trình sau:
\(\frac{{x - 1}}{{x + 1}} = 0\) và x2 – 1 = 0.
Xem lời giải »
Câu 4:
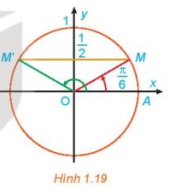
a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng [0; 2π).
b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.
Xem lời giải »
Câu 5:
a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng [– π; π).
b) Dựa vào tính tuần hoàn của hàm số côsin, hãy viết công thức nghiệm của phương trình đã cho.
Xem lời giải »
Câu 6:
Giải các phương trình sau:
a) 2cos x = \( - \sqrt 2 \);
b) cos 3x – sin 5x = 0.
Xem lời giải »
Câu 7:
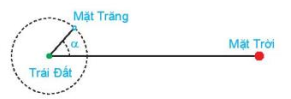
Khi Mặt Trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng một phần. Các pha của Mặt Trăng mô tả mức độ phần bề mặt của nó được Mặt Trời chiếu sáng. Khi góc giữa Mặt Trời, Trái Đất và Mặt Trăng là α (0° ≤ α ≤ 360°) thì tỉ lệ F của phần Mặt Trăng được chiếu sáng cho bởi công thức
\(F = \frac{1}{2}\left( {1 - \cos \alpha } \right)\).
(Theo trang usno.navy.mil).
Xác định góc α tương ứng với các pha sau của Mặt Trăng:
a) F = 0 (trăng mới);
b) F = 0,25 (trăng lưỡi liềm);
c) F = 0,5 (trăng bán nguyệt đầu tháng hoặc trăng bán nguyệt cuối tháng);
d) F = 1 (trăng tròn).
Xem lời giải »
Câu 8:
a) Quan sát Hình 1.24, hãy cho biết đường thẳng y = 1 cắt đồ thị hàm số y = tan x tại mấy điểm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)?
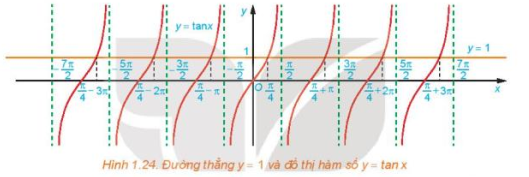
b) Dựa vào tính tuần hoàn của hàm tang, hãy viết công thức nghiệm của phương trình đã cho.
Xem lời giải »



