Tìm giá trị của tham số m để hàm số f( x ) = sin xn^e 'u, x lớn hơn bằng 0; - x + m, n^e 'u, x < 0 liên tục trên ℝ.
Câu hỏi:
Tìm giá trị của tham số m để hàm số
\(f\left( x \right) = \left\{ \begin{array}{l}\sin \,x\,\,\,\,\,\,\,\,\,\,\,\,n\^e 'u\,\,x \ge 0\\ - x + m\,\,\,\,\,\,n\^e 'u\,\,x < 0\end{array} \right.\)
liên tục trên ℝ.
Trả lời:
Lời giải:
Tập xác định của hàm số là ℝ.
+) Nếu x > 0, thì f(x) = sin x. Do đó nó liên tục trên (0; +∞).
+) Nếu x < 0, thì f(x) = – x + m, đây là hàm đa thức nên nó liên tục trên (–∞; 0).
Khi đó, hàm số f(x) liên tục trên các khoảng (–∞; 0) và (0; +∞).
Do đó, để hàm số f(x) liên tục trên ℝ thì f(x) phải liên tục tại x = 0. Điều này xảy ra khi và chỉ khi \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right)\) \( \Leftrightarrow \mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = f\left( 0 \right)\) (1).
Lại có: \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \sin \,x = 0\); f(0) = sin 0 = 0; \(\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( { - x + m} \right) = m\).
Khi đó, (1) ⇔ m = 0.
Vậy m = 0 thì thỏa mãn yêu cầu bài toán.
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết:
Câu 1:
Một người lái xe từ địa điểm A đến địa điểm B trong thời gian 3 giờ. Biết quãng đường từ A đến B dài 180 km. Chứng tỏ rằng có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h.
Xem lời giải »
Câu 2:
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\,\,\,\,\,\,n\^e 'u\,\,\,\,\,x \ne 1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,n\^e 'u\,\,\,\,\,x = 1.\end{array} \right.\)
Tìm giới hạn \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) và so sánh giá trị này với f(1).
Xem lời giải »
Câu 3:
Xét tính liên tục của hàm số \(f\left( x \right) = \left\{ \begin{array}{l} - x\,\,\,\,n\^e 'u\,\,x < 0\\0\,\,\,\,\,\,\,\,n\^e 'u\,\,x = 0\\{x^2}\,\,\,\,\,n\^e 'u\,\,x > 0\end{array} \right.\) tại điểm x0 = 0.
Xem lời giải »
Câu 4:
Cho hai hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x\,\,\,n\^e 'u\,\,0 \le x \le \frac{1}{2}\\1\,\,\,\,\,\,\,\,n\^e 'u\,\,\,\frac{1}{2} < x \le 1\end{array} \right.\) và \(g\left( x \right) = \left\{ \begin{array}{l}x\,\,\,n\^e 'u\,\,0 \le x \le \frac{1}{2}\\1\,\,\,\,n\^e 'u\,\,\frac{1}{2} < x \le 1\end{array} \right.\) với đồ thị tương ứng như Hình 5.7.
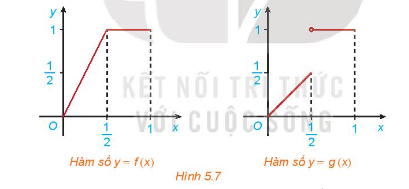
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm \(x = \frac{1}{2}\) và nhận xét về sự khác nhau giữa hai đồ thị.
Xem lời giải »
Câu 5:
Một bảng giá cước taxi được cho như sau:
|
Giá mở cửa
(0,5 km đầu)
|
Giá cước các km tiếp theo đến 30 km
|
Giá cước từ km thứ 31
|
|
10 000 đồng
|
13 500 đồng
|
11 000 đồng
|
a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển.
b) Xét tính liên tục của hàm số ở câu a.
Xem lời giải »