Cho hai hàm số f( x ) = 2x, n^e 'u0 nhỏ hơn bằng x nhỏ hơn bằng 1/2; 1 n^e'u 1/2 < x nhỏ hơn bằng 1 và g( x ) = x; n^e'u; 0 nhỏ hơn bằng x nhỏ hơn bằng 1/2 1; n^e 'u, 1/2 < x nhỏ hơn bằng 1 v

Cho hai hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x\,\,\,n\^e 'u\,\,0 \le x \le \frac{1}{2}\\1\,\,\,\,\,\,\,\,n\^e 'u\,\,\,\frac{1}{2} < x \le 1\end{array} \right.\) và \(g\left( x \right) = \left\{ \begin{array}{l}x\,\,\,n\^e 'u\,\,0 \le x \le \frac{1}{2}\\1\,\,\,\,n\^e 'u\,\,\frac{1}{2} < x \le 1\end{array} \right.\) với đồ thị tương ứng như Hình 5.7.

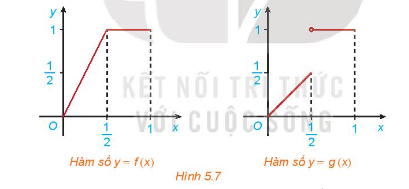
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm \(x = \frac{1}{2}\) và nhận xét về sự khác nhau giữa hai đồ thị.

Lời giải:

+) Hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x\,\,\,n\^e 'u\,\,0 \le x \le \frac{1}{2}\\1\,\,\,\,\,\,\,\,n\^e 'u\,\,\,\frac{1}{2} < x \le 1\end{array} \right.\).

Hàm số f(x) xác định trên [0; 1], do đó \(x = \frac{1}{2}\) thuộc tập xác định của hàm số.

Ta có: \(\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} 1 = 1\); \(\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} \left( {2x} \right) = 2 \cdot \frac{1}{2} = 1\).

Suy ra \(\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} f\left( x \right) = 1\), do đó \(\mathop {\lim }\limits_{x \to \frac{1}{2}} f\left( x \right) = 1\)

Mà \(f\left( {\frac{1}{2}} \right) = 2 \cdot \frac{1}{2} = 1\) nên \(\mathop {\lim }\limits_{x \to \frac{1}{2}} f\left( x \right) = f\left( {\frac{1}{2}} \right)\).

Vậy hàm số f(x) liên tục tại \(x = \frac{1}{2}\).

+) Hàm số \(g\left( x \right) = \left\{ \begin{array}{l}x\,\,\,n\^e 'u\,\,0 \le x \le \frac{1}{2}\\1\,\,\,\,n\^e 'u\,\,\frac{1}{2} < x \le 1\end{array} \right.\).

Hàm số g(x) xác định trên [0; 1], do đó \(x = \frac{1}{2}\) thuộc tập xác định của hàm số.

Ta có: \(\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} g\left( x \right) = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} x = \frac{1}{2}\); \(\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} g\left( x \right) = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} 1 = 1\)

Suy ra \(\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} g\left( x \right) \ne \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} g\left( x \right)\).

Vậy không tồn tại giới hạn của hàm số g(x) tại \(x = \frac{1}{2}\), do đó hàm số g(x) gián đoạn tại \(x = \frac{1}{2}\).

+) Quan sát Hình 5.7 ta thấy, đồ thị của hàm số y = f(x) là đường liền trên (0; 1), còn đồ thị của hàm số y = g(x) trên (0; 1) là các đoạn rời nhau.