Trong Vật lí, ta biết rằng phương trình tổng quát của một vật dao động điều hòa cho bởi công thức x(t) = Acos(ωt + φ), trong đó t là thời điểm (tính bằng giây), x(t) là li độ của vật tại thời
Câu hỏi:
Trong Vật lí, ta biết rằng phương trình tổng quát của một vật dao động điều hòa cho bởi công thức x(t) = Acos(ωt + φ), trong đó t là thời điểm (tính bằng giây), x(t) là li độ của vật tại thời điểm t, A là biên độ dao động (A > 0), ωt + φ là pha của dao động tại thời điểm t và φ ∈ [–π; π] là pha ban đầu của dao động. Dao động điều hòa này có chu kì \(T = \frac{{2\pi }}{\omega }\) (tức là khoảng thời gian để vật thực hiện một dao động toàn phần).
Giả sử một vật dao động điều hòa theo phương trình x(t) = – 5cos 4πt (cm).
a) Hãy xác định biên độ và pha ban đầu của dao động.
b) Tính pha của dao động tại thời điểm t = 2 (giây). Hỏi trong khoảng thời gian 2 giây, vật thực hiện được bao nhiêu dao động toàn phần?
Trả lời:
Lời giải:
a) Ta có: – 5cos 4πt = 5cos(4πt + π).
Khi đó vật dao động điều hòa theo phương trình x(t) = 5cos(4πt + π) (cm) với biên độ dao động là A = 5 > 0 và pha ban đầu của dao động là φ = π.
b) Pha của dao động tại thời điểm t = 2 (giây) là ωt + φ = 4π . 2 + π = 9π.
Dao động điều hòa có chu kì là \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = \frac{1}{2} = 0,5\), có nghĩa là khoảng thời gian để vật thực hiện một dao động toàn phần là 0,5 giây. Do đó, trong khoảng thời gian 2 giây, vật thực hiện được 2 : 0,5 = 4 dao động toàn phần.
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết:
Câu 1:
Giả sử vận tốc v (tính bằng lít/giây) của luồng khí trong một chu kì hô hấp (tức là thời gian từ lúc bắt đầu của một nhịp thở đến khi bắt đầu của nhịp thở tiếp theo) của một người nào đó ở trạng thái nghỉ ngơi được cho bởi công thức
\(v = 0,85\sin \frac{{\pi t}}{3}\),
trong đó t là thời gian (tính bằng giây). Hãy tìm thời gian của một chu kì hô hấp đầy đủ và số chu kì hô hấp trong một phút của người đó.
Xem lời giải »
Câu 2:
Hoàn thành bảng sau:
|
x
|
sin x
|
cos x
|
tan x
|
cot x
|
|
\(\frac{\pi }{6}\)
|
?
|
?
|
?
|
?
|
|
0
|
?
|
?
|
?
|
?
|
|
\( - \frac{\pi }{2}\)
|
?
|
?
|
?
|
?
|
Xem lời giải »
Câu 3:
Tìm tập xác định của hàm số \(y = \frac{1}{{\sin x}}.\)
Xem lời giải »
Câu 4:
Cho hai hàm số f(x) = x2 và g(x) = x3, với các đồ thị như hình dưới đây.
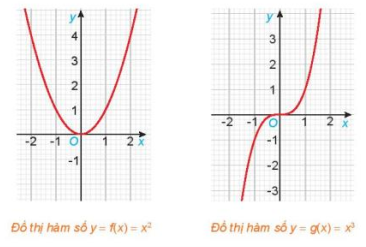
a) Tìm các tập xác định Df, Dg của các hàm số f(x) và g(x).
b) Chứng tỏ rằng f(– x) = f(x), ∀ x ∈ Df. Có nhận xét gì về tính đối xứng của đồ thị hàm số y = f(x) đối với hệ trục tọa độ Oxy?
c) Chứng tỏ rằng g(– x) = – g(x), ∀ x ∈ Dg. Có nhận xét gì về tính đối xứng của đồ thị hàm số y = g(x) đối với hệ trục tọa độ Oxy?
Xem lời giải »
Câu 5:
Cho hàm số y = tan x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = tan x trên khoảng \(\left( { - \frac{\pi }{2};\,\frac{\pi }{2}} \right)\).
|
x
|
\( - \frac{\pi }{3}\)
|
\( - \frac{\pi }{4}\)
|
\( - \frac{\pi }{6}\)
|
0
|
\(\frac{\pi }{6}\)
|
\(\frac{\pi }{4}\)
|
\(\frac{\pi }{3}\)
|
|
y = tan x
|
?
|
?
|
?
|
?
|
?
|
?
|
?
|
Bằng cách lấy nhiều điểm M(x; tan x) với x ∈ \(\left( { - \frac{\pi }{2};\,\frac{\pi }{2}} \right)\) và nối lại ta được đồ thị hàm số y = tan x trên khoảng \(\left( { - \frac{\pi }{2};\,\frac{\pi }{2}} \right)\).
c) Bằng cách làm tương tự câu b cho các khoảng khác có độ dài bằng chu kì T = π, ta được đồ thị của hàm số y = tan x như hình dưới đây.
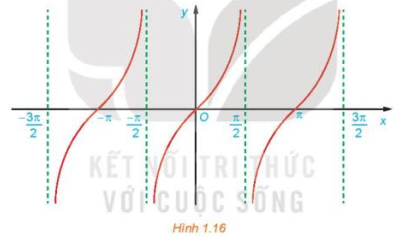
Từ đồ thị ở Hình 1.16, hãy tìm tập giá trị và các khoảng đồng biến của hàm số y = tan x.
Xem lời giải »
Câu 6:
Sử dụng đồ thị đã vẽ ở Hình 1.16, hãy xác định các giá trị của x trên đoạn \(\left[ { - \pi ;\,\frac{{3\pi }}{2}} \right]\) để hàm số y = tan x nhận giá trị âm.
Xem lời giải »
Câu 7:
Cho hàm số y = cot x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = cot x trên khoảng (0; π).
|
x
|
\(\frac{\pi }{6}\)
|
\(\frac{\pi }{4}\)
|
\(\frac{\pi }{3}\)
|
\(\frac{\pi }{2}\)
|
\(\frac{{2\pi }}{3}\)
|
\(\frac{{3\pi }}{4}\)
|
\(\frac{{5\pi }}{6}\)
|
|
y = cot x
|
?
|
?
|
?
|
?
|
?
|
?
|
?
|
Bằng cách lấy nhiều điểm M(x; cot x) với x ∈ (0; π) và nối lại ta được đồ thị hàm số y = cot x trên khoảng (0; π).
c) Bằng cách làm tương tự câu b cho các khoảng khác có độ dài bằng chu kì T = π, ta được đồ thị của hàm số y = cot x như hình dưới đây.
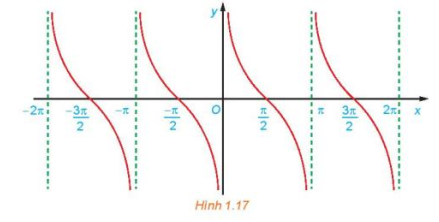
Từ đồ thị ở Hình 1.17, hãy tìm tập giá trị và các khoảng nghịch biến của hàm số y = cotx.
Xem lời giải »
Câu 8:
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn \(\left[ { - \frac{\pi }{2};\,2\pi } \right]\) để hàm số y = cot x nhận giá trị dương.
Xem lời giải »



